Схемы включения

Для ёмкостных преобразователей применяют два принципиально различных вида измерительных схем — амплитудные и частотные. Первые обеспечивают преобразование ёмкости в амплитуду выходного переменного напряжения. Вторые представляют собой колебательный контур, входящий в состав измерительного генератора, и преобразуют изменение ёмкости в изменение частоты выходного напряжения.

Обычно ёмкостные датчики питают переменным током высокой частоты $\omega=2\pi f$, которая должна значительно превышать наибольшую частоту $\Omega$ изменения ёмкости под действием измеряемой величины. Ёмкости большинства преобразователей составляют 10–100 пФ, и поэтому даже при относительно высоких частотах питающего напряжения ($f=10^{5}–10^{7}Гц$) их выходные сопротивления велики и равны $|Z_{C}|=1/\omega C\approx 10^{3}–10^{6} Ом$. Выходные мощности ёмкостных преобразователей, напротив, невелики, и в измерительных цепях необходимо применение усилителей. Допустимые значения напряжения питания ёмкостных преобразователей достаточно велики, и напряжение питания, как правило, ограничивается не возможностями преобразователя, а условиями реализации измерительной цепи.

Оценим параметры простейшего преобразователя малых перемещений, схематическая конструкция которого и эквивалентная схема показаны на рисунке.

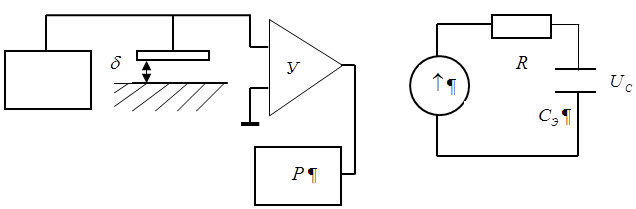
Здесь $\tilde{U}=U_{0}e^{j\omega t}$ — напряжение питающего генератора; $C_{Э}=C_{0}+C_{n}+C_{У}^{вх}$; $C_{0}$ — собственная ёмкость преобразователя; $C_{n}$ — паразитные ёмкости монтажа и электрического кабеля; $C_{У}^{вх}$ — входная ёмкость усилителя; $R$ — выходное сопротивление генератора (значениями сопротивления изоляции кабеля, сопротивления утечки между электродами и входного сопротивления усилителя пренебрежём).

Очевидно, отношение напряжения на электродах датчика $\tilde{U}_{C}$ к питающему напряжению $\tilde{U}$ определяет частотный коэффициент передачи, равный:

$$\frac{\tilde{U}_{C}}{\tilde{U}}=K(j\omega)=\frac{1}{1+j\omega RC_{Э}}$$

(12.6)

С учётом формулы ёмкости плоского конденсатора (13.1) получим, что чувствительность датчика по напряжению будет зависеть от частоты следующим образом:

$$S=\left|\frac{dU}{d\delta}\right|=\left|\frac{\partial U}{\partial C}\frac{\partial C}{\partial \delta}\right|=\frac{U_{0}}{\delta}\frac{\omega RC}{(1+\omega ^{2}R^{2}C^{2})}$$

(12.7)

Определим частоту питания датчика, соответствующую максимуму чувствительности, из условия: $dS/d\omega=0$. Отсюда получаем: $\omega RC+1$, или $\omega=1/RC$.

Для датчика с параметрами: воздушный зазор $\delta =0,1$ мм, площадь пластины $S_{0}=1$ cм$^{2}$, $R\sim Z=10^{4}$ Ом, получим частоту питания $\omega =10^{7}$ 1/c. При напряжении питания $U_{0}=100$ B ей будет соответствовать чувствительность датчика, равная $U_{0}/2\delta =500$ B/мм.

На практике достижение такой высокой чувствительности затруднено рядом причин: необходимостью обеспечения равномерности малого зазора в диапазоне единиц и десятков $мкм$, возможным изменением межэлектродного зазора вследствие линейного расширения под действием температуры, наличием паразитных ёмкостей, тоже зависящих от температуры, наконец, необходимостью защиты измерительных цепей от наводок. Для уменьшения погрешностей измерительные цепи, включая усилитель сигналов, располагают вблизи датчика.

Для включения недифференциального ёмкостного преобразователя может использоваться резонансная цепь. Генератор через разделительный трансформатор питает резонансный $LC$ — контур, ёмкость которого состоит из ёмкости преобразователя $C_{пр}$ и ёмкости подстроечного конденсатора $C^{*}$. При изменении ёмкости напряжение на контуре изменяется по резонансной кривой. Изменение ёмкости датчика на $\Delta C$ изменяет напряжение на контуре на $\Delta U$. Подстроечный конденсатор обеспечивает настройку контура так, чтобы чувствительность измерительной цепи $S=\Delta U/\Delta C$ была максимальной. Чувствительность резонансной цепи довольно высока и увеличивается с увеличением добротности контура.

Дифференциальные ёмкостные датчики включают преимущественно в мостовые измерительные цепи, позволяющие уменьшить аддитивные составляющие температурных погрешностей и получить линейную характеристику в достаточно большом диапазоне перемещений при увеличении чувствительности вдвое.

Достоинства ёмкостных датчиков — простота конструкции, малые размеры и масса, высокая чувствительность, возможность измерения быстропеременных величин в широком интервале частот делают их незаменимым инструментом в научных исследованиях. Однако особенности их использования в сложных условиях измерений (высокие и низкие температуры, ионизирующие излучения) требуют высокой квалификации персонала.

3/3