Принцип действия индуктивного датчика перемещений

Имеются два класса преобразователей: с изменяющейся индуктивностью и с изменяющимся активным сопротивлением. Пример схемы преобразователя первого класса показан на рис. $1$а.

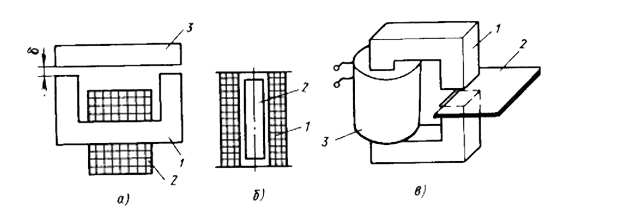
Рис. 1

Преобразователь состоит из П–образного сердечника (магнитопровода) $1$, на котором размещена катушка $2$, и подвижного якоря 3. При перемещении якоря изменяется длина воздушного зазора $\delta$ и, следовательно, магнитное сопротивление, что вызывает изменение индуктивности катушки датчика, которая может быть зарегистрирована. Возможен вариант преобразователя, в конструкции которого якорь перемещается горизонтально относительно П–образного сердечника и изменяет эффективную площадь замыкания магнитного потока. Оба варианта датчика: и с переменным зазором, и с переменной площадью — относятся к датчикам с замкнутой магнитной цепью.

Другая широко используемая модификация первого класса относится к датчикам с разомкнутой магнитной цепью. Пример такого датчика, называемого соленоидным или плунжерным преобразователем, показан на рис. $1$б. Преобразователь представляет собой катушку $1$, из которой может выдвигаться ферромагнитный сердечник $2$ (плунжер). При среднем положении плунжера индуктивность максимальна. Этот тип преобразователя применяется для измерения значительных перемещений сердечника (до $100$ мм).

Схема преобразователя второго класса приведена на рис. $1$в. В зазор магнитной цепи $1$ вводится пластинка $2$ с высокой электропроводностью, в которой наводятся вихревые токи, приводящие к увеличению потерь активной мощности катушки $3$. Это приводит к изменению составляющих полного комплексного сопротивления катушки индуктивности, в частности, к увеличению её активного сопротивления, что тоже может быть зарегистрировано. Этот тип датчика будет рассмотрен в классе вихретоковых преобразователей.

Определим функцию преобразования датчика на примере преобразователя с переменным зазором (рис. $1$а). Как известно, индуктивность катушки $L$ определяется соотношением: $L=wФ/I$, где $w$ — число витков; $Ф$ — пронизывающий её магнитный поток; $I$ — проходящий по катушке ток. С учётом $Ф=Iw/Z_М$, получим:

$$L=\frac{w^2}{Z_м},$$

(14.2)

где $Z_м$ — полное сопротивление магнитному потоку, которое состоит из двух составляющих: магнитного сопротивления сердечника $Z_{мс}$ и магнитного сопротивления воздушных зазоров $R_3$. Если пренебречь рассеянием магнитного потока и нелинейностью кривой намагничивания сердечника (они будут учтены в форме потерь на вихревые токи и магнитный гистерезис как составляющие сопротивления потерь $R_п$), то

$$Z_М= R_С+R_3=\frac{l}{\mu \mu_0 S_C}+\frac{2\delta}{\mu _0 S_3},$$

(14.3)

где $R_C$ — суммарное магнитное сопротивление участков магнитопровода; l — длина средней силовой линии по участкам магнитопровода; $S_C$ — их поперечное сечение; $\mu$ — магнитная проницаемость материала сердечника; $\mu_{0}=4\pi\cdot10^{-7}$Гн/м — магнитная постоянная; $\delta$ и $S_3$ — соответственно длина и сечение воздушного зазора. Отсюда:

$$L=\frac{\mu_0w^2}{\frac{l}{\mu S_C}+\frac{2\delta}{S_3}}.$$

(14.4)

Так как $ S_C\approx S_3 = S_0$, а для удовлетворительной работы датчика требуется выполнение условия $2\delta\gg l/\mu$, что достигается выбором для магнитопровода материала с большим значением магнитной проницаемости $\mu\geq 10^3$, то окончательно получаем:

$$L\approx \mu_0w^2S_0/2\delta$$

(14.5)

и полное комплексное сопротивление $Z$ катушки запишется в виде:

$$Z=R_П+j\omega L\approx R_П+ j\omega \mu_0 w^2 S_0/2\delta.$$

(14.6)

Модуль полного комплексного сопротивления катушки индуктивности часто записывают в виде:

$$|Z|=\sqrt{R_П^2+(\omega L)^2}=\omega L\sqrt{1+\frac{1}{Q^2}},$$

(14.7)

где Q $= \omega L/R_П$ — добротность индуктивного датчика, характеризуемая отношением запасённой энергии в контуре к энергии рассеянной. Значения Q для разных сердечников такие — сталь: Q = $1$ − $4$; пермаллой: Q = $3$ − $10$; ферриты: Q = $3$ − $20$;

Из выражения (14.6) оценим чувствительность датчика с переменным зазором:

$$S=\left|\frac{\partial Z}{\partial L}\right|\left|\frac{\partial L}{\partial \delta}\right|=\omega \sqrt{1+1/Q^2}\cdot \frac{\mu _0 w^2 S_0}{2 \delta^2}$$

(14.8)

В ряде случаев чувствительность индуктивного преобразователя удобно характеризовать величиной:

$$S\approx\frac{\Delta Z/Z}{\Delta \delta}=\frac{1}{Z}\cdot \frac{dZ}{d\delta}=1/\delta,$$

(14.9)

из которой следует существенное возрастание чувствительности датчика с уменьшением протяжённости воздушного зазора $\delta$. Из $(14.9)$ следует, что относительное изменение индуктивности датчика равно:

$$\frac{\Delta L}{L}=\frac{\Delta Z}{Z}=\frac{\Delta \delta}{\delta}.$$

(14.10)

Последнее выражение позволяет оценить порог чувствительности индуктивных датчиков перемещений. Современные измерительные схемы и приборы позволяют измерить относительное изменение индуктивности $\Delta L/L$ с точностью до $0,1–0,01$ %, что соответствует относительному изменению зазора $\Delta\delta/\delta$ = $10^{-3} - 10^{-4}$. При номинальной величине зазора $\delta_0$ = $0,5$ мм минимальные перемещения, которые могут быть зарегистрированы, равны $0,5 – 0,05$ мкм.

3/5