Техника и методы физических измерений и расчётов
3. Математические модели сигналов Спектр амплитуд периодической последовательности прямоугольных импульсов
Скачать Содержание

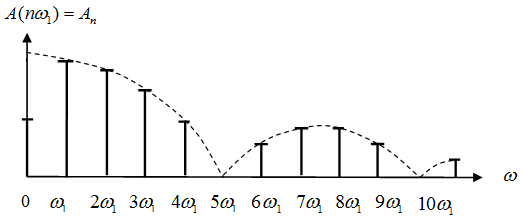
Спектр амплитуд периодической последовательности прямоугольных импульсов


Опре­де­лим спектр ам­пли­туд пе­ри­о­ди­че­ской по­сле­до­ва­тель­но­сти пря­мо­уголь­ных им­пуль­сов дли­тель­но­стью τ и ам­пли­ту­дой U0, сле­ду­ю­щих с ча­сто­той ω1 = 2π/T (см. ри­су­нок):

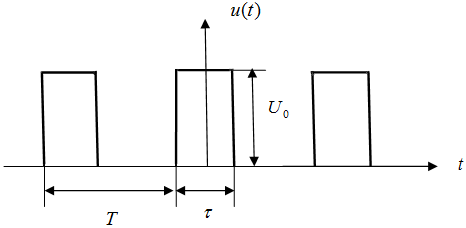
За­пи­шем u(t) в ви­де ря­да Фу­рье в со­от­вет­ствии с вы­ра­же­ни­ем (3.2):

(3.10)

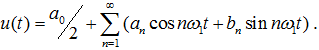
Ко­эф­фи­ци­ен­ты раз­ло­же­ния най­дем по фор­му­лам (3.3) – (3.5). При этом вве­дем па­ра­метр 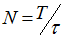, на­зы­ва­е­мый скваж­но­стью им­пульс­ной по­сле­до­ва­тель­но­сти.

Зна­че­ния ко­эф­фи­ци­ен­тов рав­ны:

(3.11)
(3.12)

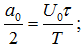
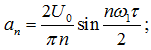
bn = 0, т. к. функ­ция u(t)  — чёт­ная, и A(nω1) = An = |an|.

Отсюда

(3.13)

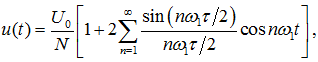
а ам­пли­ту­ды гар­мо­ник, вклю­чая по­сто­ян­ную со­став­ля­ю­щую A0/2, опре­де­ля­ют­ся из вы­ра­же­ния:

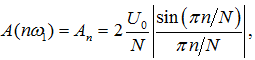при n = 0,1,2,...
(3.14)

Ана­лиз за­ви­си­мо­стей (3.11) – (3.13) по­ка­зы­ва­ет:

  • При боль­ших зна­че­ни­ях скваж­но­сти им­пульс­ной по­сле­до­ва­тель­но­сти (N ≫ 1), ам­пли­туд­ный спектр сиг­на­ла со­дер­жит боль­шое чис­ло мед­лен­но убы­ва­ю­щих по ам­пли­ту­де гар­мо­ник. При этом рас­сто­я­ние меж­ду со­сед­ни­ми ли­ни­я­ми ма­ло, а ам­пли­ту­ды со­сед­них гар­мо­ник близ­ки по ве­ли­чи­не.
  • Зна­че­ние по­сто­ян­ной со­став­ля­ю­щей A0/2при­мер­но вдвое мень­ше ам­пли­ту­ды пер­вой гар­мо­ни­ки A1.
  • На ча­сто­тах, крат­ных 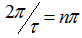, оги­ба­ю­щая спек­тра рав­на ну­лю. Сле­до­ва­тель­но, ам­пли­ту­да гар­мо­ник, чей но­мер кра­тен скваж­но­сти N, бу­дет рав­на ну­лю.
  • •Оги­ба­ю­щая спек­тра ам­пли­туд опре­де­ля­ет­ся ви­дом функ­ции
(3.15)

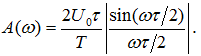
При­мер спек­траль­ной диа­грам­мы пе­ри­о­ди­че­ской по­сле­до­ва­тель­но­сти пря­мо­уголь­ных им­пуль­сов для скваж­но­сти N = 5 при­ве­дён на ри­сун­ке:

5/5