Частотная форма представления периодических сигналов
Математической моделью процесса, повторяющегося во времени, является периодический сигнал: s(t) = s(t ± nT), n = 1, 2, 3, ... Здесь T — период сигнала. Ставится задача найти спектральное разложение такого сигнала.
Введём основную частоту ω1 = 2π/T последовательности, образующей периодический сигнал. Ряд Фурье для периодического сигнала будет иметь вид:
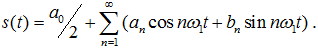
Коэффициенты разложения функции в ряд Фурье находят по формулам:


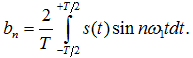
Таким образом, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами ωn = nω1(n = 1, 2, 3, ...), кратными основной частоте ω1.
Каждую гармонику можно описать ее амплитудой An и начальной фазой φn. Для этого коэффициенты ряда Фурье следует записать в виде an = An cos φn, bn = An sin φn так что

Подставив эти выражения в (3.1), получим другую, эквивалентную форму ряда Фурье:

Ряд Фурье для периодического сигнала s(t) может быть записан в форме:
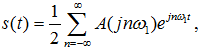
где
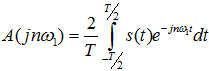
Соотношение (3.6) представляет собой ряд Фурье в комплексной форме, содержащий экспоненциальные функции как с положительным, так и с отрицательным параметром ω (двустороннее частотное представление). Составляющие с «отрицательными частотами» являются следствием комплексной формы записи вещественной функции.
Функцию A(jnω1) принято называть комплексным спектром периодического сигнала s(t). Этот спектр — дискретный, или линейчатый, так как функция A(jnω1) определена только для целых значений n. Значение функции A(jnω1) при конкретном n называют комплексной амплитудой. Запишем комплексный спектр в форме:

Модуль комплексного спектра A(nω1) называют спектром амплитуд, а функцию φ(nω1) — спектром фаз сигнала s(t). Спектры амплитуд и фаз периодического сигнала являются дискретными. При этом спектр амплитуд является чётной функцией n, т. е. A(nω1) = A(-nω1), а спектр фаз — нечётной функцией n, т. е. φ(nω1) = φ(-nω1).
От двухстороннего спектрального представления легко перейти к одностороннему (не имеющему отрицательных частот), объединяя комплексно-сопряжённые составляющие. В этом случае получим ряд Фурье в тригонометрической форме, ранее записанный в виде (3.2)..
Спектр амплитуд и спектр фаз периодического сигнала удобно представлять наглядно в виде спектральных диаграмм. Пример спектральной диаграммы амплитудного спектра сигнала, отображаемого совокупностью линий на частотах nω1, приведён на рисунке:
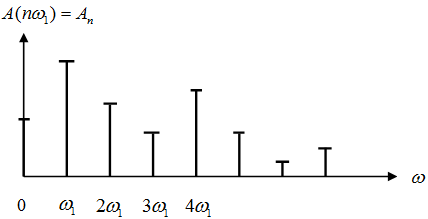
Огибающую A(ω)этого спектра амплитуд можно получить, заменив nω1 в A(nω1) на ω, где ω = nω1 для n-ой гармоники сигнала. Отметим, что дискретный (линейчатый) спектр характеризует не только периодические сигналы. Линейчатые спектры, включающие гармоники некратных частот, могут принадлежать так называемым почти периодическим сигналам.



