Физические измерительные системы и их математические модели

Ди­на­ми­че­ские из­ме­ри­тель­ные си­сте­мы, в ко­то­рых свя­зи меж­ду из­ме­ря­е­мы­ми ве­ли­чи­на­ми (вход­ны­ми сиг­на­ла­ми) и вы­ход­ны­ми сиг­на­ла­ми опи­сы­ва­ют­ся диф­фе­рен­ци­аль­ны­ми урав­не­ни­я­ми, раз­но­об­раз­ны по прин­ци­пам внут­рен­не­го устрой­ства и внеш­ним ха­рак­те­ри­сти­кам. В об­щем ви­де ма­те­ма­ти­че­ская мо­дель та­кой си­сте­мы мо­жет быть за­пи­са­на сле­ду­ю­щим об­ра­зом:

(6.1)

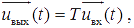
где T — си­стем­ный опе­ра­тор, ре­зуль­та­том воз­дей­ствия ко­то­ро­го на сиг­нал 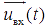яв­ля­ет­ся 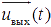. В об­щем слу­чае вход­ной сиг­нал пред­став­ля­ет­ся в ви­де m-мер­но­го век­то­ра 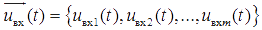, а вы­ход­ной сиг­нал — в ви­де n-мер­но­го век­то­ра 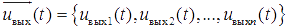. Стро­го го­во­ря, что­бы пол­но­стью за­дать ма­те­ма­ти­че­скую мо­дель си­сте­мы, опи­сы­ва­е­мой вы­ра­же­ни­ем (6.1), сле­ду­ет ука­зать об­ласть до­пу­сти­мых вход­ных воз­дей­ствий D_вх и об­ласть до­пу­сти­мых вы­ход­ных сиг­на­лов D_вых.