Динамические характеристики линейных стационарных систем
Дифференциальное уравнение линейной системы, описывающее связь между мгновенными значениями входного и выходного сигналов, имеет вид:
Если динамическая система линейна и стационарна, то все коэффициенты этого уравнения ai и bj — постоянные вещественные числа. Порядок n этого уравнения (n ≥ m всегда) принято называть порядком динамической системы. Используя интегральные преобразования Фурье и Лапласа для решения уравнения (6.4), а также типовые входные воздействия на систему, можно получить динамические характеристики самой системы: частотную характеристику, передаточную функцию, импульсную и переходную характеристики.
Частотная характеристика линейной системы
Применяя к правой и левой частям уравнения (6.4) прямое преобразование Фурье и используя известное свойство для производных функций, получим:
Введём коэффициент, определяемый как отношение преобразованных по Фурье выходного сигнала к входному:
Коэффициент K(jω) называют частотной характеристикой динамической системы или частотным коэффициентом передачи.
Итак, частотная характеристика динамической системы, описываемой обыкновенными дифференциальными уравнениями с постоянными коэффициентами, представляет собой дробно-рациональную функцию переменной jω. Коэффициенты этой функции совпадают с коэффициентами дифференциального уравнения. Значения этих коэффициентов определяются физическими свойствами и параметрами динамической системы, а их знание позволяет найти K(jω).
Из (6.6) следует, что при известном (регистрируемом) сигнале на выходе измерительной системы и известной частотной характеристике K(jω) нетрудно получить с помощью обратного преобразования Фурье функцию, характеризующее входное воздействие на эту систему:
Частотную характеристику системы K(jω) удобно представлять в форме:
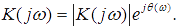
Модуль |K(jω)| = K(ω) называют амплитудно-частотной характеристикой (АЧХ) системы, а аргумент θ(ω)— фазочастотной характеристикой (ФЧХ) системы. Если записать K(jω) в виде K(jω) = A(ω) - jB(ω), то АЧХ и ФЧХ системы могут быть записаны в виде вещественных функций, исходя из соотношений:
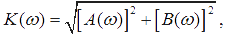
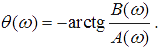
Очевидно, что амплитудно-частотная характеристика системы является чётной функцией частоты, а фазочастотная характеристика системы — нечётной функцией частоты.
Физическая реализуемость систем
Далеко не каждая функция K(jω) может являться частотным коэффициентом передачи физически реализуемой системы. Простейшее ограничение связано с тем, что K(jω) должна быть чётной функцией частоты, т. е. K(jω) = K*(– jω). Сложнее записать условие физической осуществимости системы. Запишем без доказательства критерий Пэли-Винера: частотный коэффициент передачи физически реализуемой системы должен быть таким, чтобы существовал интеграл:
Другие критерии физической реализуемости будут введены позже.
Методы определения K(jω)
В инженерных расчётах частотную характеристику (частотный коэффициент передачи) линейных систем часто находят методами теории цепей на основании принципиальных схем, не прибегая к составлению дифференциальных уравнений. Рассмотрим примеры расчётов применительно к простейшим линейным цепям, содержащим пассивные элементы — резисторы и конденсаторы. Такие цепи широко применяют для преобразований сигналов, имеющих характер дифференцирования или интегрирования.
Рассмотрим RC–цепь, на вход которой подан импульсный сигнал вида uвх(t).
Соотношения, связывающие значения входного и выходного сигналов с параметрами RC-цепи, очевидны:
Используя выражение (6.6), определяем частотную характеристику RC-цепи как отношение преобразованных по Фурье выходного сигнала к входному:
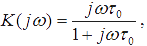
где τ0 = RC — постоянная времени RC-цепи.
Далее находим модуль (АЧХ) и аргумент (ФЧХ) частотной характеристики:
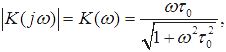
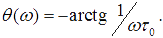
Проанализируем полученные выражения с точки зрения выполнения операции приближённого дифференцирования сигнала. При точном дифференцировании сигнала, описываемом соотношением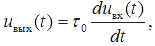 
частотная характеристика идеального дифференциатора должна иметь вид: Kид(jω) = jωτ0, а модуль частотной характеристики — Kид(ω) = ωτ0 Очевидно, что эти условия для реальной RC-цепи будут выполняться, если произведение ωτ0 будет пренебрежимо малым по сравнению с единицей для всех частот спектра входного сигнала, в том числе и для самой верхней. Пусть входной сигнал — прямоугольный видеоимпульс длительностью τи. Используя грубую оценку верхней граничной частоты в спектре такого импульса 
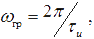получаем условие пригодности RC-цепи для приближённого дифференцирования данного сигнала:
Диаметрально противоположными свойствами будет обладать RC–цепь, если в схеме поменять местами резистор и конденсатор:
Частотная характеристика такой RC-цепи запишется в виде:
а АЧХ и ФЧХ этой цепи будут иметь вид:
Операция точного интегрирования функции uвх(t) аналитически записывается в виде:
Тогда частотная характеристика идеального интегратора должна иметь вид:
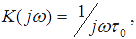
а АЧХ идеального интегратора:
АЧХ RC-цепи приведена на следующем рисунке:
Приближённое интегрирование RC–цепью будет выполняться тем точнее, чем больше относительная доля высокочастотных составляющих в спектре сигнала. Другими словами, условие ωτ0 ≫ 1 должно выполняться для всех частот, в том числе и для самых низких.
Как следует из рисунка, интегрирующие свойства RC-цепи дают возможность подавлять высокочастотные составляющие спектра входного сигнала и поэтому такая цепь может быть использована в качестве фильтра низких частот.
Частотный коэффициент передачи многозвенной системы
В измерительной технике часто используют сложные системы, отдельные звенья которых (преобразователи, функциональные блоки) включены каскадно (последовательно), т. е. выходной сигнал предыдущего звена служит входным сигналом для последующего. Если известны частотные коэффициенты передачи отдельных звеньев Ki(jω), i = 1, 2, ..., n, то результирующий коэффициент передачи будет равен:
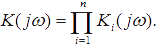
В целом применение аппарата преобразований Фурье к анализу прохождения сигналов через линейные стационарные системы позволяет говорить о спектральном подходе к описанию таких систем. В соответствии с (6.6) частотная характеристика системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и выходе. Следовательно, анализ систем в частотной области сводится к простым алгебраическим операциям Фурье-преобразованных сигналов на входе и выходе системы и её частотной характеристики.
