Угловая модуляция

Как отмечалось, угловая модуляция включает в себя две разновидности: фазовую модуляцию (ФМ) и частотную (ЧМ). При фазовой модуляции модулирующая функция $x(t)$ воздействует непосредственно на фазу гармонического сигнала, а при частотной модуляции функция $x(t)$ воздействует непосредственно на частоту, а изменение фазы является следствием изменения частоты. Так как , т. е. угловая частота есть скорость изменения фазы колебаний, то $φ (t)=\int\limits_0^t \omega (t)dt + φ _{0}$ — полная фаза есть интегральное значение круговой частоты.

При ЧМ мгновенная частота равна:

$$\omega (t)=\omega _{0}+\Delta \omega x(t),$$

(8.10)

где $\Delta \omega$ — девиация частоты, равная максимальному изменению частоты в результате ЧМ, и ЧМ сигнал запишется в виде:

(8.11)

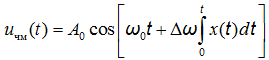
Отсюда модуляция частоты по закону $x(t)$ приводит к модуляции фазы по закону $\int\limits_0^t x(t)dt $.

При ФМ модуляции:

$$u_{фм}(t)=A_{0}\mathrm{cos}[\omega _{0}t+\Delta φ x (t)]$$

(8.12)

При этом мгновенная частота сигнала

$$\omega (t)=\frac{d\psi (t)}{dt}=\omega _{0}+\Delta φ\frac{dx(t)}{dt}$$

(8.13)

где $\Delta φ$ — девиация фазы, т. е. максимальное изменение начальной фазы при ФМ.

Таким образом, модуляция фазы по закону $x(t)$ приводит к модуляции частоты по закону $dx(t)/dt$, и по внешнему виду невозможно отличить ФМ сигналы от ЧМ сигналов.

5/5