Тональная амплитудная модуляция

Тональной называется модуляция, при которой модулирующая функция имеет вид гармонического сигнала с частотой $\Omega \ll \omega _{0}:xt=\mathrm{cos}\Omega t$

При рассмотрении тональной амплитудной модуляции для упрощения записи будем считать начальные фазы сигналов равными нулю. Тогда мгновенное значение АМ сигнала запишется в виде:

$$u(t)=A_{0}[1+m\mathrm{cos} \Omega t]\mathrm{cos}(\omega _{0}t)$$

(8.4)

Используя известную тригонометрическую формулу произведения косинусов, из выражения $(8.4)$ получим:

$$u(t)=A_{0}\mathrm{cos}(\omega _{0}t)+\frac{1}{2}mA_{0}\mathrm{cos}(\omega _{0}-\Omega)t+\frac{1}{2}mA_{0}\mathrm{cos}(\omega _{0}+\Omega)t$$

(8.5)

Формула $(8.5)$ устанавливает спектральный состав тонального АМ сигнала. Видно, что спектр АМ сигнала содержит частотные компоненты несущего сигнала $\omega _{0}$ и двух боковых частот: $(\omega _{0}-\Omega)$ и $(\omega _{0}+\Omega)$.

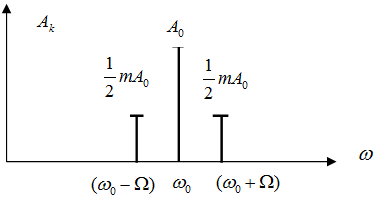
При построении спектральной диаграммы тонального АМ сигнала (см. рисунок) следует обратить внимание на равенство амплитуд верхнего и нижнего боковых колебаний (при этом их значения не могут превышать половины амплитуды немодулированного сигнала) и на симметрию расположения этих спектральных составляющих относительно несущего сигнала. Важно, что спектр АМ сигнала не содержит спектральной составляющей с частотой модулирующей функции $x(t)$. Очевидно, что ширина спектра АМ сигнала равна $2\Omega$, то есть вдвое превышает ширину спектра модулирующей функции.

Свойство симметрии спектра АМ сигнала позволяет использовать при необходимости разновидность АМ — однополосную амплитудную модуляцию, при которой передаётся только одна боковая полоса (вторая боковая подавляется). В этом случае вдвое сокращается ширина спектра АМ сигнала.

Аналогичные результаты можно получить при модуляции носителя любым сложным сигналом. Если модулирующая низкочастотная функция имеет сложный спектральный состав, например:

$$x(t)=\sum_{i=1}^n\alpha _{i}\mathrm{cos}(\Omega _{i}t+φ _{i}),$$

(8.6)

где частоты $\Omega _{i}$ образуют упорядоченную возрастающую последовательность $\Omega _{1}\lt \Omega _{2}\lt...\lt \Omega _{n}$, а амплитуды $\alpha _{i}$ и начальные фазы $φ _{i}$ произвольны, то подставляя $(8.6)$ в ($8.3)$ получим:

$$U_{AM}(t)=A_{0}[1+\sum_{i=1}^n m\alpha _{i}\mathrm{cos}(\Omega _{i}t+φ _{i})]\mathrm{cos}(\omega _{0}t+φ _{0})$$

(8.7)

Введём совокупность парциальных (частичных) коэффициентов модуляции $M_{i}=m\alpha _{i}$ и запишем аналитическое выражение сложномодулированного (многотонального) АМ сигнала в форме:

$$U_{AM}(t)=A_{0}[1+\sum_{i=1}^n M _{i}\mathrm{cos}(\Omega _{i}t+φ _{i})]\mathrm{cos}(\omega _{0}t+φ _{0})$$

(8.8)

Спектральное разложение такого сигнала имеет вид:

$$u_{AM}(t)=A_{0}\mathrm{cos}(\omega _{0}t+φ _{0})+\frac{A_{0}}{2}\sum_{i=1}^n M_{i}\mathrm{cos}[(\omega _{0}-\Omega _{i})t+φ _{0}-φ _{i}]+$$ $$+\frac{A_{0}}{2}\sum_{i=1}^n M_{i}\mathrm{cos}[(\omega _{0}+\Omega _{i})t+φ _{0}+φ _{i}]$$

(8.9)

Очевидно, что в спектре сложно модулированного АМ сигнала, помимо несущего сигнала, содержатся две группы верхних и нижних боковых частот, являющиеся масштабной копией спектра модулирующей функции, сдвинутой в область высоких частот на величину $\omega _{0}$, и располагающиеся зеркально относительно несущей частоты $\omega _{0}$.

Если спектр модулирующей функции не линейчатый, а сплошной и сосредоточен в низкочастотной области, то общие закономерности амплитудной модуляции сохраняются:

огибающая АМ сигнала связана с мгновенными значениями низкочастотной модулирующей функции;
спектр АМ сигнала образуется несущей частотой и двумя всплесками, зеркально отражаемыми относительно частоты $\omega _{0}$;
полоса частот, необходимая для передачи АМ сигнала, равна удвоенному значению наивысшей частоты (граничной частоты $\omega _{гр}$ спектра модулирующей функции; при этом необходимо выполнение условия $\omega _{гр}\ll\omega _{0}$.

Таким образом, процесс амплитудной модуляции связан с переносом спектра исходного сигнала из области низких частот в область высоких частот. В измерительной технике это необходимо в следующих случаях:

если среда, используемая для передачи сообщений, физически не может переносить сигналы низких частот, соответствующих спектру функции $x(t)$, а может переносить сигналы более высоких частот (например, радиоканалы);
при наличии в диапазоне частот, соответствующих спектру $x(t)$, сильных помех или шумов (перенос сообщений в область более высоких частот устраняет или уменьшает влияние этих помех или шумов);
при использовании кабельной линии для одновременной передачи нескольких сообщений вида $x(t)$ от различных источников, если эти сигналы имеют перекрывающиеся частотные спектры, (модуляция носителей с различными частотами $\omega _{0}$ позволяет разнести спектры сигналов).

На практике амплитудная модуляция реализуется либо в линейной цепи с переменными параметрами, либо в нелинейной цепи. Из выражения $(8.3)$ следует, что амплитудный модулятор должен выполнять операцию перемножения двух функций: $[1+mx(t)]$ и $A_{0}\mathrm{cos}(\omega _{0}t+φ _{0})$. Следовательно, амплитудный модулятор должен представлять собой аналоговое перемножающее устройство. Наиболее просто АМ в линейной цепи с переменными параметрами реализуется на транзисторах или операционных усилителях с управляемым коэффициентом усиления.

После регистрации или передачи АМ сигнала по каналу связи необходимо осуществить его демодуляцию (детектирование), т. е. выделить модулирующую функцию, которая в неявном виде содержится в модулированном высокочастотном сигнале. По своему назначению детектирование является процессом, обратным процессу модуляции, т. е. детектирование тоже сопровождается трансформацией частотного спектра и не может быть осуществлено без применения нелинейных цепей или же линейных цепей с переменными параметрами. Амплитудный демодулятор можно представит в виде сочетания детектора (диода) с фильтром нижних частот ФНЧ:

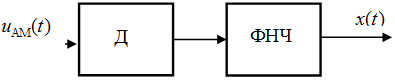
В детекторе происходит выделение среднего значения выходного напряжения, а ФНЧ подавляет высокочастотные составляющие $\omega _{0}$.

4/5