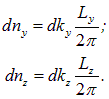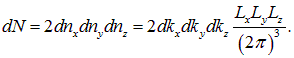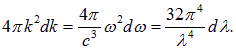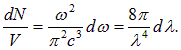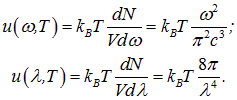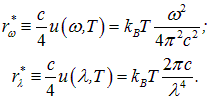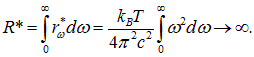1.3. Классические результаты для теплового излучения

Несмотря на детальное изучение характеристик теплового излучения, математический вид функций  и  долгое время оставался для физиков загадкой.

Попытка строгого теоретического вывода зависимости  принадлежит английским ученым Дж. Рэлею и Дж. Джинсу. Воспроизведем их аргументы. Пусть полость представляет собой прямоугольный ящик с линейными размерами L_x, L_y, L_z вдоль соответствующих координатных осей. Рассмотрим стоячие электромагнитные волны вдоль оси х. Эти волны эквивалентны стоячим волнам, возникающим в струне. Их длины волн  должны удовлетворять соотношению

откуда для проекции волнового вектора находим

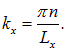
Число  нумерует разные типы волн, существующих на струне длины L_x. Поэтому число типов стоячих электромагнитных волн с проекциями волнового вектора в интервале от k_x до k_x + dk_x равно

Мы уменьшили результат в два раза, потому что стоячие волны с волновыми числами k_x и –k_x — это одно и то же колебание (направления распространения для стоячих волн не существует).

 

Рис. 1.10. Джинс Джеймс Хопвуд (1877–1946)

 

Рис. 1.11. Рэлей Джон Уильям (1842–1919)

Аналогичные формулы можно записать для стоячих электромагнитных волн вдоль осей y и z:

Перемножая эти соотношения, находим полное число типов колебаний в прямоугольной полости, волновые векторы которых лежат в интервале от  до  

Здесь мы увеличили результат в два раза, чтобы учесть поперечность электромагнитных волн: при данной длине волны колебания могут осуществляться в двух взаимно ортогональных направлениях.

Учитывая, что частота определяется только модулем волнового вектора и не зависит от его направления, перейдем к сферическим координатам, проинтегрируем по углам (учтем все направления), то есть произведем замену

Тогда выражение (1.14) для  приобретет вид:

   

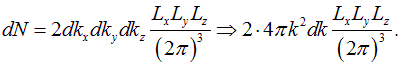
Учитывая, что

получаем (опуская знак «минус»)

Произведение

есть объем полости. Находим тогда для числа типов колебаний, приходящихся на единичный объем:

Далее Рэлей и Джине применили классическую теорему о равнораспределении энергии по степеням свободы, согласно которой на каждую степень свободы в классической статистической системе приходится энергия

(здесь k_B — постоянная Больцмана). У гармонического осциллятора средняя кинетическая энергия равна средней потенциальной, и поэтому его средняя энергия равна k_BТ. Аналогично в электромагнитной волне колеблются векторы напряженностей электрического и магнитного поля, которые дают одинаковый вклад в средний поток энергии. Поэтому для спектральной плотности энергии излучения Рэлей и Джине нашли выражения:

Соответственно, для испускательной способности абсолютно черного тела были получены соотношения:

Для длинных волн формула Рэлея — Джинса дает хорошее совпадение с экспериментальными данными, но для коротких волн, то есть в области больших частот, расчетные значения спектральной плотности  перестают совпадать с экспериментом (кривая уходит на бесконечность). Кроме того, энергетическая светимость черного тела также получается бесконечной:

Создавшееся положение было названо «ультрафиолетовой катастрофой». Таким образом, классическая физика оказалась не в состоянии объяснить важные экспериментальные данные.