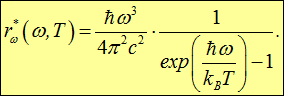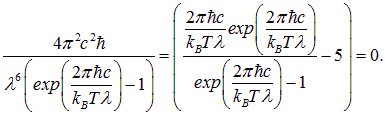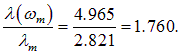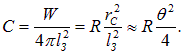1.4. Закон излучения Планка

М. Планк указал выход из создавшегося положения, выдвинув гипотезу, что электромагнитная энергия испускается и поглощается не непрерывно, а отдельными порциями (квантами)

Коэффициент пропорциональности в соотношении между энергией  и частотой света  в СИ измеряется в Дж∙с и называется теперь постоянной Планка. Впоследствии было установлено ее численное значение:

В соответствии с гипотезой Планка, энергия  рассмотренной выше стоячей волны в резонаторе может принимать лишь дискретный набор значений

кратных частоте волны.

 

Рис. 1.12. Планк Макс Карл Эрнст Людвиг (1858–1947)

Используя это соотношение, Планк получил аналитическое выражение для испускательной способности черного тела. Для излучения в состоянии термодинамического равновесия по-прежнему справедливо распределение Больцмана. Соответственно, вероятность Р_n того, что энергия стоячей волны с частотой  равна

определяется формулой

Сумма всех вероятностей равна единице, откуда мы находим нормировочный коэффициент С:

Средняя энергия колебания с частотой w равна

Метод расчета таких сумм основан на выражении для суммы членов геометрической прогрессии и формулы, получаемой из нее дифференцированием:

Подставляя сюда

находим выражение для средней энергии стоячей волны

Умножая число стоячих волн в единице объема и с частотой в интервале  на их среднюю энергию (1.25), получаем формулу Планка для спектральной плотности энергии теплового излучения

Испускательная способность абсолютно черного тела с учетом формулы (1.6) описывается законом Планка

При высоких температурах (малых частотах)

экспоненту в знаменателе формул (1.25) и (1.27) можно разложить в ряд:

откуда получаем классическое выражение для средней энергии осциллятора

и формулу Рэлея — Джинса (1.19). Для спектральной плотности энергии и испускательной способности абсолютно черного тела в зависимости от длины волны   имеем

Оказалось, что закон Планка точно согласуется с экспериментальными данными во всем интервале длин волн, в то время как формула Рэлея — Джинса, как уже говорилось, соответствует данным опыта только при больших длинах волн (рис. 1.13).

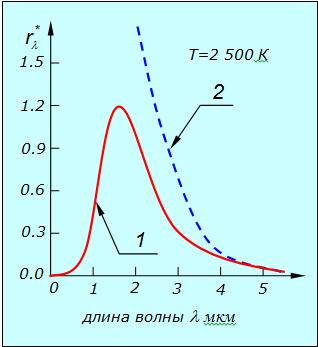
Рис. 1.13. Сравнение испускательной способности черного тела  ,
согласно закону Планка и эксперименту (1) и формуле Рэлея — Джинса (2)

Более того, из закона Планка непосредственно получается закон Стефана — Больцмана:

Введем безразмерную переменную интегрирования

В результате этого получаем

Используя значение интеграла

находим аналитическое выражение для постоянной Стефана — Больцмана:

величина которой согласуется с приведенными экспериментальными данными.

Из закона Планка следует также закон смещения Вина. Если продифференцировать функцию Планка (1.28) по , и приравнять нулю производную, то можно найти положение максимума функции . Действительно, приравнивая нулю функцию , получаем

Введя безразмерную переменную

приходим к уравнению

Корень этого уравнения

позволяет получить закон смещения Вина:

 

Рис. 1.14. Распределение Планка для испускательной способности абсолютно чёрного тела при разных температурах. С ростом температуры максимум спектров сдвигается вдоль пунктирной линии в строну коротких длин волн в соответствии с законом Вина

Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе все эмпирические законы теплового излучения, а также позволяет вычислить константы в этих законах.

Мы искали максимум функции  по длинам волн. Но излучение черного тела можно характеризовать также и распределением (1.27)  по частотам. Найдем для сравнения максимум этого распределения. Для этого надо найти экстремум функции (1.27):

Вводя безразмерную переменную

получаем уравнение для точки максимума распределения :

которое имеет корень

Отсюда следует, что максимум интенсивности  приходится на частоту

Этой частоте соответствует длина волны

которая, конечно, не определяет максимум функции (1.28) и поэтому не совпадает с выражением (1.34) для  из закона смещения Вина:

Пример 1. Принимая, что Солнце излучает как абсолютно черное тело, вычислим его энергетическую светимость и температуру поверхности. Солнечный диск виден с Земли под углом  рад. Поток солнечной энергии на земной орбите (так называемая солнечная постоянная) равен С = 1.4 кВт/м².

Пусть радиус Солнца равен r_C , а расстояние до Земли есть l_З . Их отношение связано с угловым диаметром Солнца:

Если энергетическая светимость Солнца есть R, то полная энергия, излучаемая Солнцем в единицу времени, равна произведению R на площадь поверхности Солнца:

Эта энергия достигает орбиты Земли, где она распределяется по большей площади . Отсюда находим солнечную постоянную

В итоге получаем

По формуле Стефана — Больцмана находим температуру верхних слоев Солнца

Пример 2. В пророчестве Исайи (Ис. 30, 26) сказано:

«И свет луны будет, как свет солнца, а свет солнца будет светлее всемеро, как свет семи дней, в тот день, когда Господь обвяжет рану народа Своего и исцелит нанесенные ему язвы».

Оценим температуру окружающей среды в этот день.

Поток солнечного излучения, падающий на Землю, компенсируется энергией, излучаемой Землей. Из условия задачи следует, что в указанный день поток энергии (с учетом света Луны) в восемь раз превысит нынешний поток солнечного излучения. В состоянии теплового равновесия во столько же раз должен увеличиться поток тепловой энергии с Земли. Из закона Стефана — Больцмана следует, что температура на Земле должна возрасти в

Если нынешняя средняя температура составляет 17° С = 290 К, то при увеличении потока энергии в 8 раз она составит Т = 1,68 ·290 = 487 К = 214 °С. Жарко будет!

Пример 3. Исходя из данных примера 1, найдем длину волны, на которую приходится максимум энергии солнечного излучения.

Выше была найдена температура верхних слоев Солнца. По закону смещения Вина получаем

Видео 1.4. Существуют ли лучи холода?