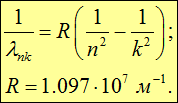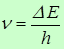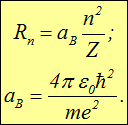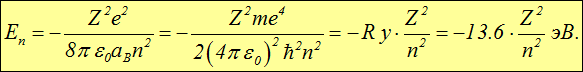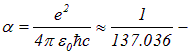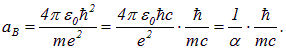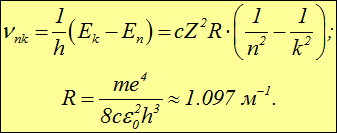3.1. Атом Бора
Вернемся в 1911 год. К этому времени дискретность микромира проявилась наиболее ярко в атомных спектрах. Оказалось, что атомы поглощают и испускают свет только определенной длины волны, причем спектральные линии группируются в так называемые серии (рис. 3.1).

Рис. 3.1. Длины волн, излучаемые атомом водорода: спектр состоит из серий (показаны три первые) —
последовательностей линий, сгущающихся к некоторому (своему для каждой серии) предельному минимальному
значению ![]() ; только четыре линии серии Бальмера лежат в видимом диапазоне
; только четыре линии серии Бальмера лежат в видимом диапазоне

Рис. 3.2. (a) Линейчатые спектры излучения газообразных водорода, ртути и гелия: (b) спектр поглощения водорода
Видео 3.1. Спектр излучения паров ртути, полученный с помощью отражательной дифракционной решетки.

Рис. 3.3. Непрерывные спектры излучения дают нагретые твёрдые и жидкие вещества, сильно сжатые газы, высокотемпературная плазма
Для спектра водорода, простейшего из атомов, была установлена (не выведена, а угадана!) несложная формула
|
|
|
(3.1) |
Здесь ![]() — длина волны излучения атома водорода, n и k > n — целые числа, R — так называемая постоянная Ридберга (
— длина волны излучения атома водорода, n и k > n — целые числа, R — так называемая постоянная Ридберга (![]() , где
, где ![]() — внесистемная единица энергии «Ридберг», равная половине атомной единице энергии). Оказалось, что серия Лаймана описывается этой формулой при значениях
— внесистемная единица энергии «Ридберг», равная половине атомной единице энергии). Оказалось, что серия Лаймана описывается этой формулой при значениях ![]() , серия Бальмера — при
, серия Бальмера — при ![]() , серия Пашена — при
, серия Пашена — при ![]() и т. д. Предельные (минимальные) значения для длин волн получаются из (3.1) при
и т. д. Предельные (минимальные) значения для длин волн получаются из (3.1) при ![]() :
:
![]()

Рис. 3.4. Йоханнес Роберт Ридберг (1854–1919)

Рис. 3.5. Теодор Лайман (1874–1954)
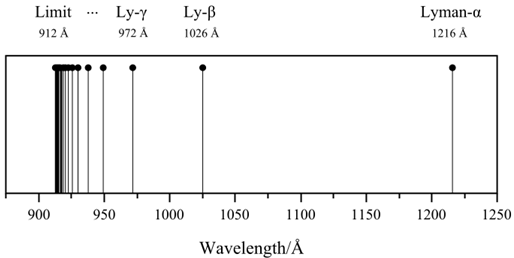
Рис. 3.6. Спектральная серия Лаймана

Рис. 3.7. Иоганн Якоб Бальмер (1825–1898)

Рис. 3.8. Видимые линии излучения водорода в серии Бальмера. Hα — красная линия справа, имеющая длину волны 656,3 нм. Самая левая линия — Hε, соответствует излучению уже в ультрафиолетовой области спектра на длине волны 397,0 нм

Рис. 3.9. Луис Карл Генрих Фридрих Пашен (1865–1947)

Рис. 3.10. Все линии серии Пашена расположены в инфракрасном диапазоне
Кроме того, в результате изучения свойств газов к тому времени было известно, что размеры атомов приблизительно
равны ![]() . Поэтому теория, объясняющая спектр и размеры атомов, должна была включать в себя какой-то параметр, позволяющий построить величину с размерностью длины (постоянных e и m — заряда и массы электрона — для этого недостаточно). Такого параметра в классической теории не было. Им могла бы стать постоянная Ридберга, но ее происхождение было темно и загадочно.
. Поэтому теория, объясняющая спектр и размеры атомов, должна была включать в себя какой-то параметр, позволяющий построить величину с размерностью длины (постоянных e и m — заряда и массы электрона — для этого недостаточно). Такого параметра в классической теории не было. Им могла бы стать постоянная Ридберга, но ее происхождение было темно и загадочно.
В 1911 году Э. Резерфорд опубликовал теоретическую работу (Rutherford E., Philosophical Magazine, v. 21, p. 669–688, 1911), в которой на базе анализа экспериментов, выполненных в 1908–1909 годах его учениками — стажером Гансом Гейгером и аспирантом Эрнстом Марсденом — (Geiger H., Marsden T., Proceedings of the Royal Society of London, Series A, v. 82, p. 495–499, 1909) утверждал наличие внутри атома положительно заряженного ядра, в котором сосредоточена практически вся масса атома.

Рис. 3.11. Эрне́ст Ре́зерфорд (1871–1937)
Видео 3.2. Немного истории. Черная шляпа и модель рассеяния.
В последствии, в одной из своих лекций сам Э. Резерфорд вспоминал о тех временах следующим образом (цитируется по книге Дж. Тригг, Решающие эксперименты в современной физике, Москва, «МИР», 1974, стр. 77): «…Я помню… ко мне пришел очень взволнованный Гейгер и сказал: «Мы, кажется, получили несколько случаев рассеяния 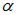 — частиц назад…». Это самое невероятное событие, которое было в моей жизни. Это почти также невероятно, как если бы вы выстрелили 15-дюймовым снарядом в папиросную бумагу и он, отразившись от неё, попал бы в вас. При анализе этого я понял, что такое рассеяние назад должно быть результатом однократного столкновения и, проведя расчеты, увидел, что это никоим образом невозможно, если не предположить, что подавляющая часть массы атома сконцентрирована в крошечном ядре. Именно тогда у меня и зародилась идея об атоме с крошечным массивным центром, в котором сосредоточен заряд». От себя добавим, что слова «рассеяние назад» фактически означали рассеяние на 150 градусов, рассеяние на большие углы не позволяла наблюдать конструкция использованной в тот момент установки.
— частиц назад…». Это самое невероятное событие, которое было в моей жизни. Это почти также невероятно, как если бы вы выстрелили 15-дюймовым снарядом в папиросную бумагу и он, отразившись от неё, попал бы в вас. При анализе этого я понял, что такое рассеяние назад должно быть результатом однократного столкновения и, проведя расчеты, увидел, что это никоим образом невозможно, если не предположить, что подавляющая часть массы атома сконцентрирована в крошечном ядре. Именно тогда у меня и зародилась идея об атоме с крошечным массивным центром, в котором сосредоточен заряд». От себя добавим, что слова «рассеяние назад» фактически означали рассеяние на 150 градусов, рассеяние на большие углы не позволяла наблюдать конструкция использованной в тот момент установки.
Принципиальная схема опытов Резерфорда представлена на рис. 3.12. Схему реальной установки можно найти в цитированной выше книге Дж. Тригга.
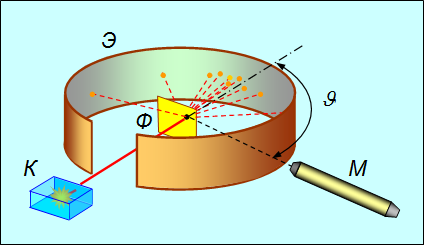
Рис. 3.12. Схема опыта Резерфорда по рассеянию 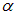 — частиц
— частиц
Видео 3.3. Натурный опыт Резерфорда на лабораторной установке.
Видео 3.4. Опыт Резерфорда «изнутри» (лабораторная установка).
Видео 3.5. Компьютерная модель опыта Резерфорда.
От радиоактивного источника, заключенного в свинцовый контейнер, ![]() частицы направлялись на тонкую фольгу Ф из исследуемого металла. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных
частицы направлялись на тонкую фольгу Ф из исследуемого металла. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных ![]() частиц в опыте Резерфорда можно было проводить под различными углами
частиц в опыте Резерфорда можно было проводить под различными углами ![]() к первоначальному направлению пучка. Было обнаружено, что большинство
к первоначальному направлению пучка. Было обнаружено, что большинство ![]() частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие
частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие ![]() частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к
частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к ![]() . Очевидно, что
. Очевидно, что ![]() частица может быть отброшена назад, только если положительный заряд атома и его масса сосредоточены в очень малом объеме внутри атома. Таким образом, было открыто атомное ядро — тело малых по сравнению с атомом размеров, в котором сосредоточен весь положительный заряд и практически вся его масса. Размеры ядра были оценены Э. Резерфордом в работе 1911 года, оценка дала меньше или порядка
частица может быть отброшена назад, только если положительный заряд атома и его масса сосредоточены в очень малом объеме внутри атома. Таким образом, было открыто атомное ядро — тело малых по сравнению с атомом размеров, в котором сосредоточен весь положительный заряд и практически вся его масса. Размеры ядра были оценены Э. Резерфордом в работе 1911 года, оценка дала меньше или порядка ![]() .
.
Видео 3.6. Прицельный параметр и форма траектории.
Видео 3.7. Заряд рассеиваемой частицы и форма траектории.
Видео 3.8. Энергия рассеиваемой частицы и форма траектории.
Видео 3.9. Заряд ядра и форма траектории.
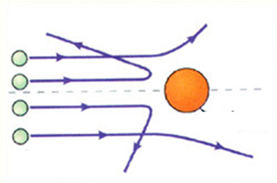
Рис. 3.13. Схема рассеяния альфа-частиц на ядре атома золота
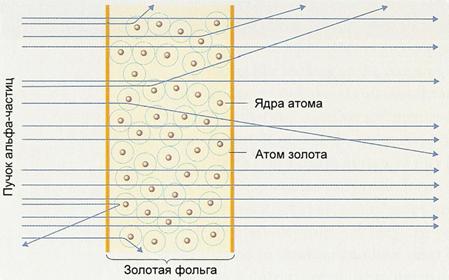
Рис. 3.14. Схема рассеяния потока альфа-частиц в тонкой золотой фольге
Возникла планетарная модель атома водорода: протон с электроном на орбите. Физики любят единые модели, а здесь так красиво в малом повторялось большое, в атоме — Солнечная система.
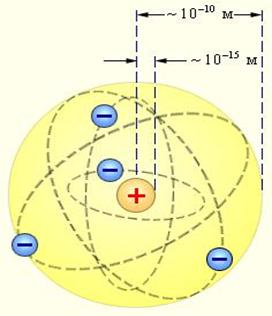
Рис. 3.15. Схема ядерной (планетарной) модели атома Резерфорда
Проблема состояла в том, что электрон, совершающий финитное, а следовательно — ускоренное движение около ядра, должен упасть на ядро. Дело в том, что электрон заряжен и при ускоренном движении должен испускать электромагнитное излучение, то есть стационарное движение невозможно. Классическая электродинамика предсказывает, что, быстро потеряв свою энергию и момент импульса орбитального движения, электрон должен упасть на ядро примерно за ![]() . Свет за это время проходит около 1.5 см (получается, что мы видим лишь «мертвые» атомы, но это не так!). Резерфорд понимал проблему, но сознательно концентрировался на факте существования ядра, полагая, что вопрос об устойчивости атома будет решен при исследовании поведения атомных электронов. Это суждено было сделать в 1913 г. Н. Бору, предложившему новую теорию атома.
. Свет за это время проходит около 1.5 см (получается, что мы видим лишь «мертвые» атомы, но это не так!). Резерфорд понимал проблему, но сознательно концентрировался на факте существования ядра, полагая, что вопрос об устойчивости атома будет решен при исследовании поведения атомных электронов. Это суждено было сделать в 1913 г. Н. Бору, предложившему новую теорию атома.
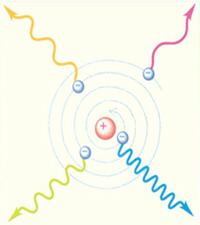
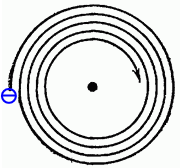
Рис. 3.16. Неустойчивость модели атома Резерфорда
Постулаты Бора
Первый постулат Бора
|
В атоме существуют стационарные орбиты, находясь на которых электрон не излучает. |
Здесь прослеживается «насильственное» введение дискретности (разрешены не все орбиты), а также типичное для физики «заметание проблемы под ковер»: если чему-то не находится объяснений, принимают это как данность и изучают следствия в надежде, что когда-нибудь поймут и причину.
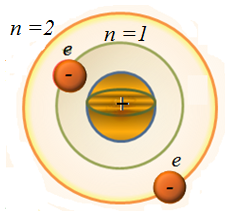
Рис. 3.17. Иллюстрация первому постулату Бора
Второй постулат Бора
|
При переходе с одной стационарной орбиты на другую электрон излучает (поглощает) квант света с частотой
( |
Этот постулат отражает сохранение энергии и соотношение Планка – Эйнштейна.
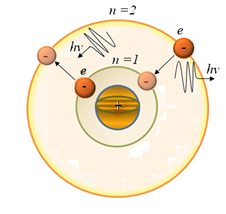
Рис. 3.18. Иллюстрация ко второму постулату Бора
Третий постулат Бора
|
Динамика электрона на стационарной орбите определяется уравнениями классической теории. |
Неизбежное следствие: так как остальные орбиты для электрона запрещены, переход осуществляется скачком; о пути и энергии электрона между орбитами говорить не имеет смысла: законы механики там не применимы.
Четвертый постулат Бора
|
Круговые стационарные орбиты определяются условием квантования момента импульса (n — целое число):
|
Постоянная Планка ħ имеет размерность момента количества движения и вместе с зарядом электрона е и его массой m позволяет образовать параметр размерности длины. Это приводит к возможности вычислить размеры атома.

Рис. 3.19. Нильс Хе́нрик Дави́д Бор (1885–1962)
Применение постулатов Бора
Классическая механика для электрона, вращающегося по круговой орбите радиусом R со скоростью v вокруг ядра с зарядом Ze, дает уравнение движения
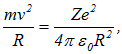
откуда
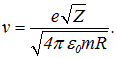
Поэтому энергия Е и момент импульса L электрона выражаются через радиус орбиты R:
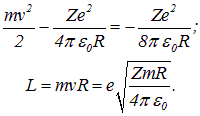
Если к последнему выражению применение условие квантования Бора L=nħ (n=1, 2, 3, …), то получатся следующие результаты.
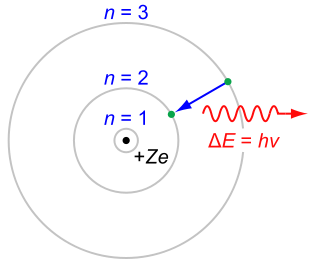
Рис. 3.20. Модель атома Бора
Характеристики водородоподобного атома
Радиусы разрешенных орбит
|
|
|
(3.2) |
Энергия электрона на стационарной орбите
|
|
|
(3.3) |
Константа аВ , имеющая размерность длины, называется радиусом Бора: ![]() . Смысл числа
. Смысл числа ![]() — номер разрешенной орбиты. Радиус Бора — радиус низшей орбиты
— номер разрешенной орбиты. Радиус Бора — радиус низшей орбиты ![]() в атоме водорода
в атоме водорода ![]() .
.
Формула (3.3) определяет дискретные значения энергии, которые может иметь электрон в атоме водорода, или, как говорят, энергетические уровни. Отрицательные значения ![]() соответствуют связанным состояниям электрона в атоме, то есть движениям в ограниченной области пространства (аналог в классической физике — движение планет по эллипсам в отличие от гиперболических и параболических траекторий, уходящих на бесконечность).
соответствуют связанным состояниям электрона в атоме, то есть движениям в ограниченной области пространства (аналог в классической физике — движение планет по эллипсам в отличие от гиперболических и параболических траекторий, уходящих на бесконечность).
При решении задач о поведении электрона в атоме обычно возникают выражения, включающие квадрат электрического заряда электрона![]() в комбинации с электрической постоянной
в комбинации с электрической постоянной ![]() . Весьма полезно ввести безразмерную комбинацию фундаментальных мировых постоянных — так называемую постоянную тонкой структуры:
. Весьма полезно ввести безразмерную комбинацию фундаментальных мировых постоянных — так называемую постоянную тонкой структуры:
|
|
|
(3.4) |
которая, совместно с атомным номером ![]() и номером орбиты
и номером орбиты ![]() , определяет масштаб релятивистских эффектов в атоме. Для того, чтобы это было лучше видно, перепишем формулу (3.3) так, чтобы в её правую часть входила постоянная тонкой структуры:
, определяет масштаб релятивистских эффектов в атоме. Для того, чтобы это было лучше видно, перепишем формулу (3.3) так, чтобы в её правую часть входила постоянная тонкой структуры:
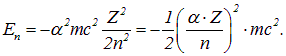
Из-за множителя ![]() характерные для атома энергии оказываются на четыре порядка меньше энергии покоя электрона. Это проявление нерелятивизма достаточно легких
характерные для атома энергии оказываются на четыре порядка меньше энергии покоя электрона. Это проявление нерелятивизма достаточно легких ![]() атомных систем. Как видно из последнего выражения в приведенной выше формуле, релятивистские эффекты перестают быть малыми поправками для ближних к ядру
атомных систем. Как видно из последнего выражения в приведенной выше формуле, релятивистские эффекты перестают быть малыми поправками для ближних к ядру ![]() электронов в тяжелых
электронов в тяжелых ![]() атомах.
атомах.
Пример 1. Определим скорость электрона на n-й орбите атома Бора. Радиус n-й орбиты определяется формулой
![]()
где аВ — радиус Бора. Скорость электрона v можно выразить через момент импульса L=nħ:
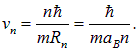
Выражение для радиуса Бора упростим, используя введенную постоянную тонкой структуры:
|
|
|
(3.5) |
Подставляя это выражение в полученную выше формулу для скорости электрона, получаем для n-й орбиты
![]()
Отсюда вытекает, что на низшей орбите скорость электрона приблизительно в 137 раз меньше скорости света, то есть атом — действительно нерелятивистская система. На n – й орбите скорости электрона в n раз меньше, чем на первой. Численный пример: на второй орбите скорость электрона равна
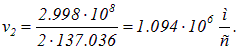
При переходе с уровня k на уровень ![]() излишек энергии
излишек энергии ![]() перейдет в энергию фотона
перейдет в энергию фотона ![]() . Поэтому для спектра излучаемых частот получаем соотношение (ср. (3.1))
. Поэтому для спектра излучаемых частот получаем соотношение (ср. (3.1))
|
|
|
(3.6) |
Таким образом, теория Бора позволила также вычислить постоянную Ридберга![]() . Стало понятно и существование спектральных серий, и предельных значений
. Стало понятно и существование спектральных серий, и предельных значений ![]() (рис. 3.21).
(рис. 3.21).

Рис. 3.21. Схема энергетических уровней и переходов в атоме водорода по теории Бора:
сплошные линии (переходы сверху вниз) — излучение, пунктирные линии (переходы снизу вверх) — поглощение.
Показаны границы (пределы) серий ![]() , которым соответствуют переходы с уровня с
, которым соответствуют переходы с уровня с
![]() — границы между континуумом и дискретным спектром
— границы между континуумом и дискретным спектром
Экспериментальное подтверждение утверждение Бора о дискретности энергетического спектра атомов нашло в опытах Франка — Герца, которые заключались в бомбардировке паров ртути электронами в вакуумной трубке и измерении зависимости анодного тока от ускоряющей разности потенциалов. Схема опыта приведена на рис. 3.22.
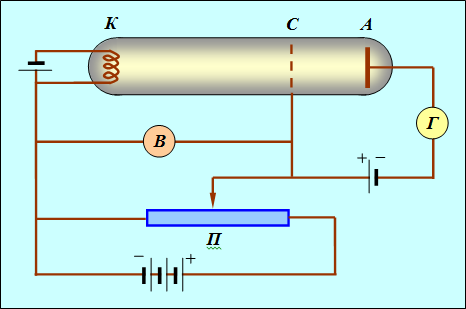
Рис. 3.22. Схема опыта Франка — Герца
В трубке, заполненной парами ртути под небольшим давлением (около 1 мм. рт. ст.), имеются три электрода: анод, катод и сетка. Электроны, вылетающие с поверхности подогретого катода вследствие термоэлектронной эмиссии, ускоряются напряжением U, приложенным между катодом и сеткой. Это напряжение можно менять с помощью потенциометра П. Между анодом и сеткой приложено слабое обратное поле с разностью потенциалов порядка 0,5ВВ , тормозящее движение электронов к аноду. Определялась зависимость тока I в цепи анода от приложенного напряжения U. Полученные результаты приведены на рис. 3.23.
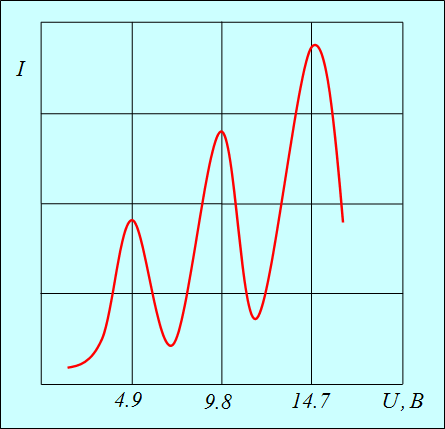
Рис. 3.23. Зависимость тока I в цепи анода от приложенного напряжения U в опыте Франка — Герца
Сила тока сначала монотонно возрастает, достигает максимума при напряжении 4,9 В, после чего с ростом U резко падает, достигает минимума и снова начинает расти. Максимумы силы тока повторяются при напряжениях 9,8 В, 14,7 В и т. д. Чередование максимумов на равном расстоянии друг от друга доказало дискретность изменения энергии атома.
Видео 3.10. Опыт Франка и Герца. Демонстрационная установка.
Видео 3.11. Опыт Франка и Герца. Сравнение ВАХ для неона и гелия.
Видео 3.12. Опыт Франка и Герца. Лабораторная установка 1.
Видео 3.12. Опыт Франка и Герца. Лабораторная установка 2.
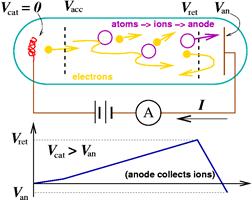
Рис. 3.24. Неупругие столкновения электронов с атомами ртути

Рис. 3.25. Джеймс Франк (1882–1964)

Рис. 3.26. Гу́став Лю́двиг Герц (1887–1975)
Пример 2. При переходе с третьего уровня на второй (головная линия серии Бальмера) водородоподобный ион атома некоторого элемента испускает фотон с энергией 7,5 эВ. Определить, какой это элемент.
Энергия электрона, находящегося на n-ой орбите около ядра с зарядом Ze, равна
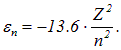
При переходе с уровня n ![]() на уровень
на уровень ![]() выделяется энергия
выделяется энергия
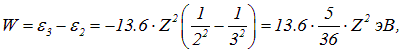
откуда
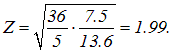
Атомный номер элемента — целое число, так что после округления получаем Z = 2, что соответствует гелию.
Как отмечалось выше, еще до появления теории Бора был изучен спектр водородного атома и эмпирически установлена формула (3.1). Но при наблюдении спектра Солнца были замечены линии, казалось бы, нарушающие эту формулу, так как они соответствовали полуцелым значениям n и k. После появления теории Бора стало ясно, что квантовые числа n и k все-таки должны быть целыми, а кажущиеся полуцелые значения можно объяснить по-другому. Действительно, из формулы (3.6) для частот, испускаемых водородоподобным атомом, следует, что
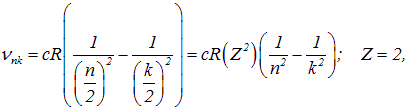
то есть наблюдавшиеся линии принадлежат иону элемента с Z = 2. Как известно, этот элемент носит «солнечное» имя — гелий.