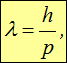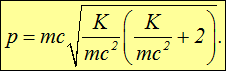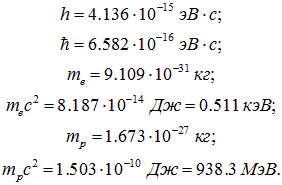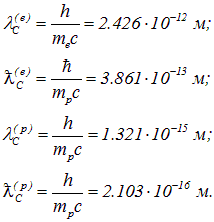3.2. Волны материи

Итак, снова дискретность, таинственные целые числа. В классической физике они появлялись в явлениях интерференции (номера максимумов и минимумов) и в стоячих волнах (число узлов на струнах). В 1923 г. была выдвинута фундаментальная гипотеза Луи де Бройля:

Рис. 3.27. Луи Виктор Пьер Раймон, 7-й герцог Брольи, более известный как Луи де Бройль (1892–1987)

Фотону мы были вынуждены приписать импульс

Долгое время уделялось внимание только его волновым свойствам, а в XX в. восстановили в правах и корпускулярные. С электроном получилось наоборот: лишь де Бройль разглядел в нем колебания с длиной волны . Условие квантования Бора

получило простую интерпретацию. Оно стало условием того, чтобы на длине стационарной орбиты уложилось целое число длин волн:

(аналогия с обоями: если по периметру комнаты укладывается целое число периодов рисунка на обоях, то при дальнейшем оклеивании рисунок воспроизводится на тех же местах — своего рода стационарность). Отсюда вытекает соотношение

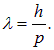
Видно, что получилась общая формула для фотонов и электронов (и любых других частиц).

Рис. 3.28. Каждую частицу (атом, молекулу) можно представить в виде волны де Бройля или волнового пакета, центр которого соответствует центру частицы. По мере охлаждения, то есть снижения скорости хаотического движения частицы, длина волны растет, и волновые пакеты частиц в конце концов перекрываются. (Изображение: «Химия и жизнь»)

Гипотеза де Бройля подтверждена экспериментами Дэвиссона и Джермера (отражение от кристаллических плоскостей) и Томсона (дифракция на фольге). Красив и поучителен опыт В.А. Фабриканта (1949 г.) — дифракция одиночных электронов, доказывающая, что волновые свойства присущи не коллективу частиц, но каждому электрону в отдельности. И в то же время электрон — частица с зарядом и массой.

 

Видео 3.13. Дифракция электронов на поликристалле.

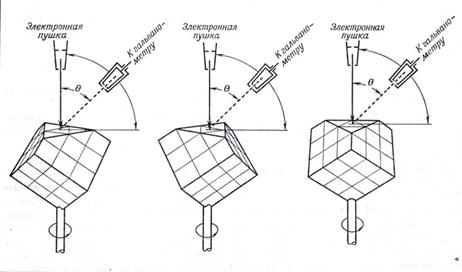
Рис. 3.29. Схема опыта Дэвиссона и Джермера по дифракции электронов (С. J. Davissоn, The discovery of electron waves, Les Prix Nobel en 1937.) На плоскость кристалла никеля, показанного в виде куба со срезанным углом, направляется пучок электронов определенной скорости. Цилиндр Фарадея, служащий для сбора дифрагированных электронов, может перемещаться по дуге вокруг кристалла. На рисунке изображены три различных положения кристалла

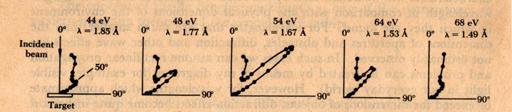
Рис. 3.30. Опыт Дэвиссона и Джермера по дифракции электронов. Полярные диаграммы интенсивности упруго рассеянных электронов для разных энергий первичного пучка

Рис. 3.31. Кли́нтон Джо́зеф Дэ́виссон (1881–1958)

Рис. 3.32. Лестер Хэлберт Джермер (1896–1971)

Рис. 3.33. Сэр Джозеф Джон Томсон (1856–1940)

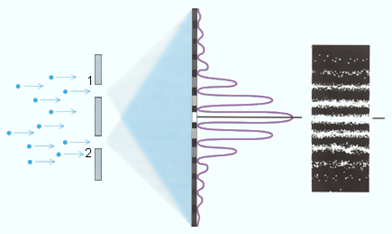
Рис. 3.34. Схема дифракции электронов на двух щелях

Рис. 3.35. Валенти́н Алекса́ндрович Фабрика́нт (1907–1991)

Вопрос, долго волновавший физиков: что такое микрочастица, волна или корпускула? Здесь налицо некорректная постановка вопроса, подразумевающая альтернативу. Надо «или» заменить на «и»: электрон и волна, и частица. Если задать этот вопрос природе с помощью прибора, то получим ответ, соответствующий прибору: для волнового прибора (например, дифракционной решетки) ответ будет «волна», для корпускулярного (скажем, счетчика) — «частица». Неоднозначность ответа отражает двойственность природы частиц или, точнее, узость нашего альтернативного мышления, допускающего лишь одну из этих возможностей. Это новые для нас объекты, квантовые русалки и кентавры микромира, которых невозможно разделить на людей и животных. В этом смысле микрообъект — не волна, не частица и не их симбиоз. Это новое качество, которое мы количественно отражаем в формуле де Бройля

связывающей волновые и корпускулярные проявления свойств единого объекта. В экспериментах с ускоренными частицами их длина волны де Бройля играет ту же роль, что и длина волны видимого света, определяющая разрешающую силу микроскопа. Ускорители — своеобразные микроскопы микромира, и с их помощью исследуются законы природы на малых расстояниях. Так, длина волны протонов, полученных на ускорителе в Серпухове, составляет примерно 10 ^–17 мм, что в 10 ⁷ раз меньше размеров атомов.

Рис. 3.36. Опыт с дифракцией нейтронов на щели шириной 90 мкм. Длина волны де Бройля для нейтронного пучка λ = 1,926 ± 0,07 ± 0,002 нм (средняя длина волны, разброс в пучке, ошибка измерения). Опыт занял около 320 часов, измерения проводились в течение двух недель на атомном реакторе с большим потоком нейтронов. На графике приведены общий вид зависимости, и она же увеличенном масштабе, чтобы лучше показать дифракционные максимумы более высокого порядка. Экспериментальные точки нанесены с указанием ошибок, сплошная кривая - результат теоретического расчета. С экспериментом согласуются и положение максимумов и их амплитуда. (Zeilinger et al. Rev. Mod. Phys., 1988, 60, 1067–1073)

При решении задач, связанных с длиной волны де Бройля, надо с осторожностью применять общую формулу (3.7). Необходимо ясно понимать, какое выражение для импульса следует использовать. Например, в задаче может быть задана скорость частицы . Если эта скорость много меньше скорости света в вакууме, то можно применить классическое соотношение

На практике считают, что , если отношение , то есть

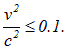
Если же это не так, то следует применить релятивистское соотношение между импульсом частицы и ее скоростью

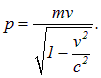
В задаче может быть задана не скорость частицы, а ее кинетическая энергия К. Критерием применимости классических формул является малость кинетической энергии по сравнению с энергией покоя частицы . Если условие

выполняется (что, как нетрудно видеть, эквивалентно условию ), то для нахождения импульса можно воспользоваться формулами классической механики

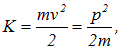
откуда

Если же кинетическая энергия частицы не мала по сравнению с энергией покоя (тем более превышает ее), то следует использовать релятивистские формулы. В теории относительности выводится общее соотношение между полной энергией частицы и ее импульсом:

откуда

Кинетическая энергия равна разности между полной энергией и энергией покоя:

так что для импульса получаем

Наконец, удобно переписать это выражение так, чтобы под знаком квадратного корня стояли безразмерные величины:

Нетрудно убедиться, что при

 

формула (3.9) действительно переходит в классическое выражение

Традиционные единицы энергии (например, Дж) оказываются неудобными в микромире. Поэтому физики предпочитают пользоваться внесистемными единицами, с которыми мы уже встречались — электрон-вольтом (эВ) и его производными (1кэВ = 10³  эВ, 1МэВ = 10⁶ эВ , 1 ГэВ  = 10⁹ эВ  и т. п.).

Так как заряд электрона равен е = 1,602·10^–19Кл , то 1 эВ = 1,602·10^–19 Дж. Поскольку у нас появилась энергия покоя, приведем ее численные значения для электрона и протона вместе с массами этих частиц. Заодно укажем численные значения постоянной Планка, выраженной в эВ·с:

Наконец, встречаются обратные задачи, когда задана длина волны де Бройля l и требуется найти скорость или энергию частицы. Возникает вопрос, как по величине  сразу определить, какими формулами следует пользоваться. Представим себе, что мы применяем для нахождения скорости классическую формулу

и, следовательно, получаем

Критерием справедливости этого результата является малость по сравнению со скоростью света в вакууме :

откуда

Комбинации констант

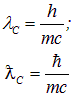
есть комптоновская длина волны частицы. По своему физическому смыслу это характерное расстояние, определяющее область , где уже неприменима нерелятивистская квантовая механика. Приведем численные значения этого важного параметра для электрона и протона:

Видно, что чем легче частица, тем больше ее комптоновская длина волны, то есть тем раньше проявятся релятивистские эффекты. Для электрона комптоновская длина волны много меньше характерной длины, определяющей размеры атома. Это значит, что к атому применима нерелятивистская квантовая механика. Ядра, состоящие из протонов и нейтронов, имеют размеры порядка 10^–14 мм, что много больше комптоновской длины волны протона. Следовательно, к ним  также применима эта теория.

Рис. 3.37. Дифракционная картина, полученная при прохождении пучка электронов (E = 75 кВ, = 0,05 А) сквозь монокристаллическую плёнку ZnSe с ориентацией (111)

Пример. Определим скорость частицы, у которой длина волны де Бройля в 10 раз меньше комптоновской длины волны .

По условию

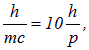
откуда находим

Так как длина волны де Бройля меньше комптоновской длины волны частицы, то мы не можем воспользоваться нерелятивистским соотношением

которое приведет к несуразному ответу =10 с (как известно, ничто не может двигаться быстрее света). Здесь необходимо применить релятивистскую формулу связи импульса со скоростью

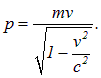
Отсюда вытекает уравнение

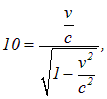
решение которого дает

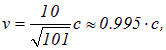
то есть скорость частицы всего на 0,5 % меньше скорости света.