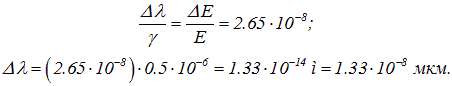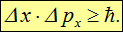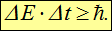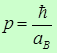3.3. Соотношения неопределенностей

Само наличие у частицы волновых свойств накладывает определенные ограничения на возможность корпускулярного описания ее поведения. Для классической частицы всегда можно указать ее точное положение и импульс. Для квантового объекта имеем иную ситуацию.

Представим цуг волн пространственной протяженностью  — образ локализованного электрона, положение которого известно с точностью . Длину волны де Бройля для электрона можно определить, подсчитав число N пространственных периодов на отрезке :

Какова точность определения ? Ясно, что для слегка отличающейся длины волны мы получим примерно то же самое значение N. Неопределенность  в длине волны ведет к неопределенности

в числе узлов, причем измерению доступны лишь . Так как

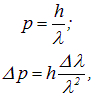
то отсюда немедленно следует знаменитое соотношение неопределенностей В. Гейзенберга для координат — импульсов (1927 г.):

Точности ради надо заметить, что, во-первых, величина  в данном случае означает неопределенность проекции импульса на ось OX и, во-вторых, приведенное рассуждение имеет скорее качественный, нежели количественный характер, поскольку мы не дали строгой математической формулировки, что понимается под неопределенностью измерения. Обычно соотношение неопределенностей для координат-импульсов записывается в виде

Аналогичные соотношения справедливы для проекций радиуса-вектора и импульса частицы на две другие координатные оси:

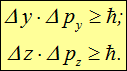
Представим теперь, что мы стоим на месте и мимо проходит электронная волна. Наблюдая за ней в течение времени , хотим найти ее частоту n. Насчитав  колебаний, определяем частоту с точностью

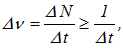
откуда имеем

или (с учетом соотношения )

Аналогично неравенству (3.12) соотношение неопределенностей Гейзенберга для энергии системы чаще используется в виде

Рис. 3.38. Ве́рнер Карл Ге́йзенберг (1901–1976)

Поговорим о физическом смысле этих соотношений. Может сложиться представление, что в них проявляется «несовершенство» макроскопических приборов. Но приборы совсем не виноваты: ограничения носят принципиальный, а не технический характер. Сам микрообъект не может быть в таком состоянии, когда определенные значения одновременно имеют какая-то из его координат и проекция импульса на ту же ось.

Смысл второго соотношения: если микрообъект живет конечное время, то его энергия не имеет точного значения, она как бы размыта. Естественная ширина спектральных липни — прямое следствие формул Гейзенберга. На стационарной орбите электрон живет неограниченно долго и энергия определена точно. В этом — физический смысл понятия стационарного состояния. Если неопределенность в энергии электрона превышает разность энергий соседних состояний

то нельзя точно сказать, на каком уровне находится электрон. Иными словами, на короткое время порядка

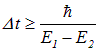
электрон может перескочить с уровня 1 на уровень 2, не излучая фотона, и затем вернуться назад. Это — виртуальный процесс, который не наблюдается и, следовательно, не нарушает закона сохранения энергии.

Похожие соотношения существуют и для других пар так называемых канонически сопряженных динамических переменных. Так, при вращении частицы вокруг некоторой оси по орбите радиусом R неопределенность ее угловой координаты  влечет за собой неопределенность ее положения на орбите . Из соотношений (3.12) следует, что неопределенность импульса частицы удовлетворяет неравенству

Учитывая связь момента импульса электрона L с его импульсом L = Rp, получаем , откуда следует еще одно соотношение неопределенностей

Некоторые следствия соотношений неопределенностей

Например, для осциллятора (тело на пружине) энергию Е можно записать в виде

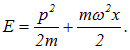
Основное состояние в классической механике это состояние покоя в положении равновесия:

Поэтому величина неопределенностей  и  имеет порядок самих значений импульса и координаты, откуда получаем

Минимум энергии достигается в точке

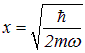
и равен

Вообще говоря, такие оценки не могут претендовать на точный ответ, хотя в данном случае (как и для атома водорода) он действительно точен. Мы получили так называемые нулевые колебания: квантовый осциллятор, в отличие от классического, не может оставаться в покое — это противоречило бы соотношению неопределенностей Гейзенберга. Точные расчеты показывают, что формулу Планка для уровней энергии осциллятора надо было бы писать в виде

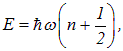
где n = 0, 1, 2, 3, ... — колебательное квантовое число.

При решении задач на применение соотношения неопределенностей следует иметь в виду, что в основном состоянии в классической физике электрон покоится в точке, соответствующей минимуму потенциальной энергии. Соотношения неопределенностей не позволяют ему это делать в квантовой теории, так что электрон должен иметь некоторый разброс импульсов. Поэтому неопределенность импульса (его отклонение от классического значения 0) и сам импульс по порядку величины совпадают

Неопределенность координаты электрона, «запертого» в объеме V, равна по порядку величины линейному размеру этого объема

Пример 1. Электрон с кинетической энергией  находится в металлической пылинке диаметром . Оценим относительную неточность dv, с которой может быть определена скорость электрона.

По условию

и

Энергия электрона много меньше его энергии покоя, так что можно применять нерелятивистские соотношения

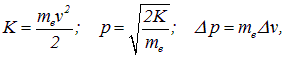
откуда

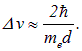
Для относительной неопределенности скорости электрона получаем

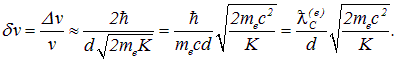
В этом выражении выделены безразмерные множители - отношение комптоновской длины волны электрона

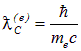
к диаметру пылинки и отношение энергии покоя электрона к его кинетической энергии. Подставляем численные значения:

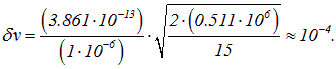
Пример 2. Среднее время жизни атома в возбужденном состоянии . При переходе в основное состояние излучается фотон с длиной волны  (зеленый цвет). Определим энергию кванта, ширину и относительную ширину спектральной линии.

Энергия кванта равна

Неопределенность в энергии определяется по соотношению

откуда

Тогда