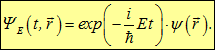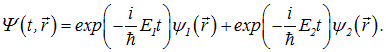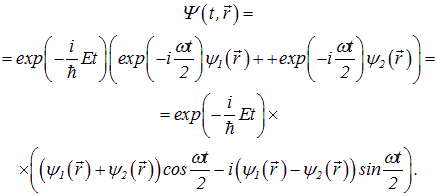4.4. Стационарное уравнение Шредингера

В теории операторов важную роль играют так называемые собственные состояния операторов. Это такие состояния, которые при действии данного оператора меняются тривиальным образом: умножаются на некоторое число. Это число называется собственным значением оператора, соответствующим данному собственному состоянию. Чтобы найти собственные состояния и собственные значения какого-то оператора, надо решить уравнение

где индекс n отличает одно решение от другого. Набор величин , то есть набор собственных значений оператора, определяет его свойства.

Рассмотрим в качестве примера операцию поворота вокруг некоторой оси .Роль состояний играют здесь обычные радиусы-векторы. Очевидно, что при повороте все векторы меняются, кроме параллельных оси. Это и есть собственные векторы оператора поворота вокруг оси , причем соответствующее собственное значение равно единице. Аналогичны выводы для поворота вокруг осей и 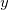. Произвольный поворот можно получить комбинацией этих трех поворотов. Соответственно, любой радиус-вектор можно представить как линейную комбинацию трех собственных векторов . Ситуация с другими операторами по сути ничем не отличается от описанной: зная набор собственных состояний , любое другое состояние  можно получить с помощью линейной комбинации, то есть с помощью принципа суперпозиции:

Связь математики с физикой реализуется в следующем правиле.

Правило 2

Следствие: в собственном состоянии  измерение 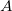с вероятностью 100 % даст значение  (так как в разложении (4.17) отличен от нуля лишь коэффициент с номером ).

Поскольку среди всех физических величин особую роль играет энергия, найдем уравнение для собственных состояний  оператора полной энергии. Уравнение, согласно сказанному, имеет вид

откуда следует решение

Мы получили общий вид состояния, в котором энергия имеет определенное значение. Такие состояния называются стационарными. Естественно, пока невозможно сказать, чему равна энергия стационарного состояния, поскольку мы еще не указали рассматриваемую физическую систему. В уравнении (4.18) стоит некая функция , не зависящая уже от времени. Она называется волновой функцией стационарного состояния. Зависимость стационарных состоянии от времени особенно проста — такая же как для свободной частицы. Отсюда следует, что в стационарном состоянии плотность вероятности не зависит от времени. В этом смысле и следует понимать название «стационарное». Подставляя решение (4.18) в общее уравнение Шредингера (4.12), получим стационарное уравнение Шредингера, то есть уравнение для :

Подчеркнем: это — уравнение для состояний с определенной энергией . В операторных обозначениях оно имеет вид

то есть представляет собой уравнение для собственных состояний гамильтониана. Задавая тот или иной вид потенциальной энергии, мы конкретизируем систему и получаем стационарное уравнение Шредингера, решения которого и описывают квантовые свойства системы.

Не следует думать, что система может быть только в стационарном состоянии. Возьмем характерный пример: пусть

и

— два неких стационарных состояния какой-то системы с разными энергиями ₁ и ₂. Предположим, что в начальный момент времени волновая функция системы является симметричной суперпозицией этих состояний:

Вопрос: что будет с системой в произвольный момент t.

Зная, что справедлив принцип суперпозиции и что зависимость собственных состояний от времени определяются соотношениями типа (4.18), можно сразу же написать волновую функцию:

Плотность вероятности такого состояния зависит от времени! Введем обозначения для средней энергии

и частоты перехода

Тогда

и легко получаем вместо (4.20)

Видно, что в момент t = 0 система находится в симметричном состоянии, к моменту времени  она перейдет в антисимметричное состояние, а в момент  — снова вернется в симметричное состояние. Следовательно, система осциллирует между симметричным и антисимметричным состояниями с круговой частотой . Здесь усматривается аналогия с классической физикой: в рассмотренной ранее системе связанных осцилляторов возникают похожие собственные колебания (нормальные моды) и биения.