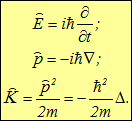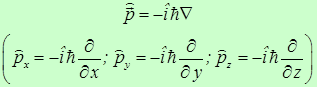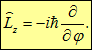4.3. Операторы, симметрия и законы сохранения

Итак, состояние электрона описывается в квантовой механике волновой функцией . Но куда подевались координаты, импульс и прочие величины, известные из классической теории? От классических представлений придется отказаться. Взамен у нас появились так называемые операторы, то есть некие операции, совершаемые над . Из уравнения Шредингера видно, что оно воспроизводит связь

полной энергии с кинетической 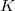и потенциальной 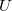, но классические величины заменены на операторы, действующие на волновую функцию . Будем обозначать оператор тем же символом, что и классическую величину, снабжая его для отличия «шляпкой». Тогда уравнение Шредингера (4.12) можно записать в операторной форме, в которой отчетливо видна его связь с энергетическими соотношениями классической физики:

где введены операторы

Здесь

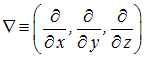
оператор градиента, квадрат которого дает оператор Лапласа . Оператор радиус-вектора сводится к простому умножению  на вектор ; то же справедливо для любой функции  (в частности, для потенциальной энергии).

Мы пришли к способу перехода от известных классических соотношений к соответствующим им квантовым: необходимо классические величины заменить в них соответству­ю­щи­ми им операторами.

Правило 1

При этом энергии частицы

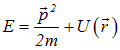
в потенциальном поле соответствует оператор полной энергии

В этих обозначениях уравнение Шредингера (4.12) имеет вид

Оператор полной энергии называется гамильтонианом (аналог функции Гамильтона в теоретической механике).

Рис. 4.7. Сэр Уи́льям Ро́уэн Га́мильтон (1805–1865)

Напомним, что в классической механике законы сохранения связаны с симметрией системы: энергия - с трансляцией (сдвигом) времени

импульс — с трансляцией пространства

момент импульса — с поворотами в пространстве (трансляцией углов)

Трансляцию какой-то обобщенной координаты 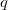производит оператор дифференцирования по этой координате. Например, для бесконечно малой трансляции

имеем по определению производной

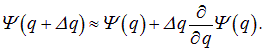
Поэтому не случайно в квантовой механике полной энергии соответствует операция взятия производной по времени

а импульсу — градиент. Аналогично оператор проекции момента импульса на какую-то ось пропорционален оператору дифференцирования

по углу поворота вокруг этой оси: