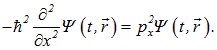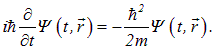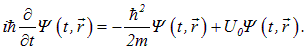4.2. Общее уравнение Шредингера

Волновая функция является главным объектом изучения в квантовой механике. Говоря о каком-то состоянии в классической физике, мы подразумевали, что в момент времени t=0 частица имела некие положение и скорость (импульс), а дальнейшая ее судьба предопределена уравнениями движения Ньютона.

Состояние в квантовой механике имеет иной смысл: в момент времени 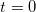задана волновая функция, изменение которой регулируется пока не известным нам уравнением (Шредингера). В этом смысле теперь понимается причинность: в классике — точные предсказания положений и скоростей, в квантовой механике — предсказания состояний (волновых функций). Уравнения новой физики (в данном случае — уравнение Шредингера) никогда не выводятся логически из прежних принципов (иначе это будет не новая теория, а следствие старой). Но квантово-механическое уравнение должно иметь некие классические корни, поскольку классическая механика хороша в области своей применимости. Далее мы приведем не вывод, но наводящие соображения (как в разд. 3.3 для соотношений неопределенностей).

Свободной частице соответствует волна де Бройля, которую мы записываем в виде классической плоской волны (в комплексной форме)

где модуль волнового вектора k связан с длиной волны соотношением

C — амплитуда. Мы использовали уже известную связь энергии и импульса частицы с частотой и длиной волны де Бройля. Искомое уравнение для волновой функции не должно содержать 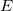и   так как это — характеристики конкретного состояния частицы. Попробуем найти операции над волновой функцией свободной частицы, позволяющие исключить параметры 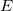и  Е и р. Имеем для производной по времени

и по пространственной координате

Такие же уравнения возникнут при дифференцировании по , 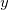и . Повторяя дифференцирование по координатам, получаем

Складывая (4.8) с аналогичными уравнениями для вторых производных по , 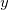и , приходим к соотношению

где знаком  обозначен оператор Лапласа:

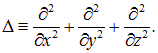
Рис. 4.6. Пьер-Симо́н Лапла́с (1749–1827)

В этом месте возникает различие между релятивистским и нерелятивистским случаями. Рассматриваемая здесь квантовая механика — нерелятивистская теория, в которой

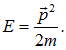
Это классическое coотношение позволяет связать дифференцирование по времени в (4.6) с дифференцированием по пространственным координатам в (4.9) и тем самым исключить из уравнения зависимость от энергии и импульса частицы:

Это уравнение вполне бы нас устроило, но написано оно пока только для свободной частицы. Легко понять, как должно выглядеть уравнение для системы с постоянным значением  потенциальной энергии. Полная энергия равна сумме

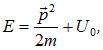
так что получаем

В случае частицы, находящейся в произвольном потенциальном поле, вблизи точки  потенциальную энергию можно считать постоянной величиной , так что искомое обобщение почти с очевидностью следует из уравнения (4.11):

Это и есть основное уравнение квантовой механики — знаменитое общее уравнение Шредингера. Подчеркнем еще раз, что вывести его строго невозможно, но можно угадать, исходя из наводящих соображений. Соответствие уравнения и его следствий физической реальности проверяется экспериментально. Уравнение Шредингера по сути есть аналог классического соотношения между полной энергией  частицы и ее кинетической энергией . Для свободной частицы они совпадают. При наличии потенциального поля это соотношение принимает вид

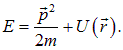
Мы уже знаем, что полной энергии соответствует производная по 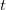, компонентам импульса — производные по x,y,z, а кинетической энергии — вторые производные по пространственным координатам, поскольку импульс входит в нее во второй степени. Классической потенциальной энергии, как мы видим, в квантовой механике соответствует обычное произведение  на волновую функцию.

Уравнение Шредингера линейно по искомой волновой функции, откуда сразу же вытекают следствия: