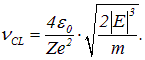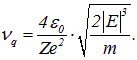4.6. Принцип соответствия Бора

Н. Бор на заре квантовой механики поставил вопрос о ее соотношении с классической. Обычные в нашем мире значения энергии велики по сравнению с характерной энергией основного состояния и расщеплением уровней: с высокой лестницы не различаем ступенек. Или, на языке квантовой механики: при больших квантовых числах (высоколежащих уровнях) должны воспроизводиться классические результаты. Покажем это на примере атома водорода.

В разд. 3.1 было получено классическое выражение для скорости электрона в атоме Бора на орбите радиусом R:

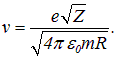
Отсюда легко получить классическую частоту вращения электрона

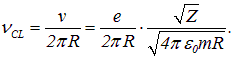
Кроме того, было найдено классическое выражение для энергии электрона на орбите

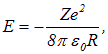
позволяющее выразить радиус орбиты через энергию электрона

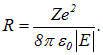
Подставляя это выражение в формулу для классической частоты вращения , получаем

Именно на этой частоте ожидается излучение электрона в классической теории.

Кроме того, в том же разделе было выведено выражение для энергии уровня с номером :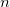

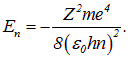
При  получаем отсюда квантовую частоту перехода  между соседними уровнями

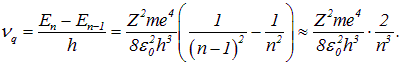
Выражая квантовое число n через энергию уровня, находим

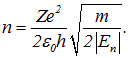
Подставляя это выражение в формулу для квантовой частоты перехода между соседними высоколежащими уровнями, приходим к окончательному результату

На этой частоте должен излучать сильно возбужденный атом Бора.

Сравнивая классическую частоту (4.29) с квантовой (4.30), убеждаемся, что при одной и той же энергии электрона они совпадают. Это свойственно не только водородоподобному атому. Аналогичный результат получается для бесконечно глубокой потенциальной ямы, этот же вывод можно сделать и для прочих систем. Следовательно, соблюдается принцип соответствия Бора:

Пример. Используя формулы и данные примера из предыдущего раздела, покажем справедливость принципа соответствия Бора для поступательного движения молекул азота в сосуде.

При переходе молекул между уровнями с разностью энергий  излучается квант света с энергией

откуда находим

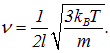
Кроме того, классическая скорость молекул азота равна

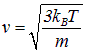
и они пролетают сосуд от стенки до стенки и обратно за время

(период классического движения). Обратная величина есть классическая частота

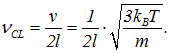
Именно на этой частоте классическая физика предсказывает электромагнитное излучение. Таким образом, принцип соответствия Бора проявляется в том, что совпадают обе частоты — квантовая (при переходах между высоковозбужденными состояниями) и классическая. То же самое справедливо, как мы видели, для атома Бора. Если подставить численные значения, то для частоты излучения в данном примере получится величина

что соответствует длине волны

— сверхдлинные радиоволны.