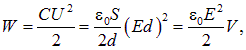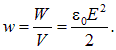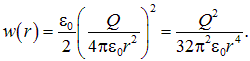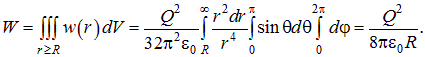2.10. Энергия электрического поля

Где же сосредоточена энергия электрического поля, запасенная в конден­саторе? Ответить на этот вопрос нам поможет только что проделанное умозрительное упражнение по зарядке плоского конденсатора «методом» раздвижения пластин. Мы совершали работу, энергия конденсатора увеличивалась, но что менялось в системе? Заряды на изолированных обкладках никуда не перетекали, напряженность электрического поля внутри конденсатора также не менялась. Единственное изменение — это увеличение объема пространства между обкладками. А в этом простран­стве у нас ничего нет, кроме электрического поля. Значит, в каждом малом объеме пространства, пронизанного силовыми линиями поля, сосредоточена какая-то энергия. Чтобы ее найти, запишем энергию плоского конденсатора таким образом, чтобы объем пространства между обкладками присутствовал явно.

Напряженность поля плоского конденсатора связана с разностью потенциалов между обкладками и величиной зазора  соотношением . Запишем энергию плоского конденсатора в виде

(2.57)

где  объем пространства между пластинами.

Так как поле в плоском конденсаторе однородно, то энергия распределена в пространстве с плотностью

(2.58)

Мы получили формулу, значение которой выходит далеко за пределы задач о конденсаторах. В сущности, конденсаторы в этой формуле уже не видны: есть напряженность электрического поля (неважно, чем создаваемая), которая определяет плотность распределения энергии, в каждой точке пространства.

Продемонстрируем это на примере поля равномерно заряженной сферы радиусом . Как мы видели выше при вычислении электромагнитного радиуса электрона, энергия электростатического поля равна

 

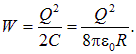
Получим этот же результат другим путем.

Напряженность поля во внешнем пространстве  как мы уже знаем, такая же, как и для точечного заряда. Поэтому плотность энергии поля равна

(2.59)

Возьмем точку в пространстве, задаваемую в сферической системе ко­ординатами  и выделим малый объем  Электростатическая энергия, сосредоточенная в этом малом объеме, равна  Полную энергию можно найти, интегрируя  по всему пространству вне сферы:

(2.60)

Полученная ранее энергия заряженной сферы теперь вычислена по ее рас­пределению в окружающем пространстве! Это — очень сильный результат, демонстрирующий, что электрическое поле не есть некая фикция или искусственный математический метод. Оно реально, оно содержит в себе энергию, которую можно измерить и употребить с пользой для себя. И это все происходит в вакууме! Проводники нужны нам как удобное хранилище для электрических зарядов, а поле и его энергия сосредоточены вне них. Значит, несмотря на отсутствие вещества, вакуум не так пуст, как это можно было бы себе представить. По крайней мере, только что мы познакомились с одной из форм существования материи, отличной от обычного осязаемого вещества.  

Задача. Получить выражение (2.51) для энергии электрона, исходя из формул (2.58).

Решение. Используя выражение для плотности электростатической энергии, получаем после простого интегрирования:

(2.61)

Естественно, мы получили тот же результат. Заметим, что из наших выкладок следует, что большая часть энергии равномерно заряженного шара приходится на окружающее его пространство: внутри шара сосредоточено лишь 16,7 % энергии.

 

Дополнительная информация

http://plato.stanford.edu/entries/equivME/ — масса и энергия, энергия покоя.