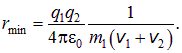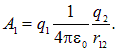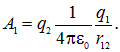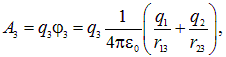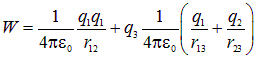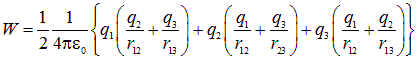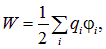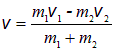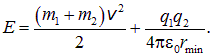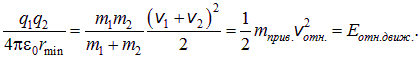2.7. Энергия системы зарядов
Система заряженных тел обладает потенциальной энергией. Рассмотрим сначала два заряда ![]() и
и ![]() находящиеся на расстоянии
находящиеся на расстоянии ![]() (рис. 2.19). При удалении одного из зарядов на бесконечность сила взаимодействия между ними уменьшается до нуля.
(рис. 2.19). При удалении одного из зарядов на бесконечность сила взаимодействия между ними уменьшается до нуля.
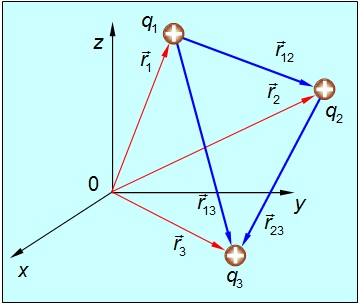
Рис. 2.19. К определению энергии системы электрических зарядов
Для сближения зарядов на расстояние ![]() необходимо совершить работу, которая идет на изменение потенциальной энергии системы. Пусть заряд
необходимо совершить работу, которая идет на изменение потенциальной энергии системы. Пусть заряд ![]() из бесконечности приближается к заряду
из бесконечности приближается к заряду ![]() на расстояние
на расстояние ![]() . Работа по его перемещению равна:
. Работа по его перемещению равна:
|
|
(2.32) |
где ![]() — потенциал поля, создаваемого зарядом
— потенциал поля, создаваемого зарядом ![]() в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд ![]() , т. е.
, т. е.
|
|
(2.33) |
Аналогично, можно считать, что из бесконечно удаленной точки приближался заряд ![]() :
:
|
|
(2.34) |
Результаты оказались одинаковыми, поскольку одинаково конечное расположение зарядов. Следовательно, потенциальная энергия взаимодействия двух зарядов равна
|
|
(2.35) |
или в симметричной форме
|
|
(2.36) |
Теперь добавим к системе зарядов ![]() и
и ![]() третий заряд
третий заряд ![]() (рис. 2.19), переносимый из бесконечности в точку, находящуюся от заряда
(рис. 2.19), переносимый из бесконечности в точку, находящуюся от заряда ![]() на расстоянии
на расстоянии ![]() и от заряда
и от заряда ![]() на расстоянии
на расстоянии ![]() . Соответствующая работа будет равна:
. Соответствующая работа будет равна:
|
|
(2.37) |
где ![]() — потенциал, создаваемый зарядами
— потенциал, создаваемый зарядами ![]() и
и ![]() в точке, где находится заряд
в точке, где находится заряд ![]() .
.
Потенциальная энергия взаимодействия трех зарядов равна:
|
|
(2.38) |
Перепишем полученное соотношение в виде:
|
|
(2.39) |
или в симметричной форме
|
|
(2.40) |
Ясно, что для произвольной системы зарядов имеем
|
|
(2.41) |
где ![]() — потенциал в точке, где находится заряд
— потенциал в точке, где находится заряд ![]() , создаваемый всеми остальными зарядами, кроме
, создаваемый всеми остальными зарядами, кроме ![]() .
.
Задача. Две одноименно заряженные частицы с зарядами ![]() и
и ![]() и массами
и массами ![]() и
и ![]() пущены с большого расстояния навстречу друг другу по соединяющей их прямой линии со скоростями
пущены с большого расстояния навстречу друг другу по соединяющей их прямой линии со скоростями ![]() и
и ![]() , соответственно. Определить наименьшее расстояние
, соответственно. Определить наименьшее расстояние ![]() , на которое могут сблизиться частицы.
, на которое могут сблизиться частицы.
Решение. Сначала ответим на вопрос: почему вообще существует минимально возможное расстояние сближения частиц, почему они не могут столкнуться друг с другом? Ответ прост: частицы отталкиваются вследствие закона Кулона и потенциальная энергия взаимодействия при ![]() возрастает до бесконечности. Начальной кинетической энергии частиц просто не хватит, чтобы преодолеть бесконечно высокий потенциальный барьер между ними. Рассмотрим процесс сближения частиц. По мере уменьшения расстояния
возрастает до бесконечности. Начальной кинетической энергии частиц просто не хватит, чтобы преодолеть бесконечно высокий потенциальный барьер между ними. Рассмотрим процесс сближения частиц. По мере уменьшения расстояния ![]() между ними растут силы отталкивания, тормозящие частицы. Скорость сближения — относительная скорость частиц — уменьшается и в какой-то момент становится равной нулю. В это мгновение частицы движутся как единое целое, их скорости одинаковы (мы обозначим их
между ними растут силы отталкивания, тормозящие частицы. Скорость сближения — относительная скорость частиц — уменьшается и в какой-то момент становится равной нулю. В это мгновение частицы движутся как единое целое, их скорости одинаковы (мы обозначим их ![]() ). Это и есть момент наибольшего сближения. Далее под влиянием отталкивания частицы снова начнут расходиться и в конечном итоге удалятся друг от друга.
). Это и есть момент наибольшего сближения. Далее под влиянием отталкивания частицы снова начнут расходиться и в конечном итоге удалятся друг от друга.
Проанализировав процесс, примемся за уравнения. В начальном состоянии полный импульс частиц равен ![]() (мы считаем, что первая частица движется в положительном направлении). В момент наибольшего сближения частицы движутся с одинаковой скоростью
(мы считаем, что первая частица движется в положительном направлении). В момент наибольшего сближения частицы движутся с одинаковой скоростью ![]() (скоростью их центра масс) и импульс системы равен
(скоростью их центра масс) и импульс системы равен ![]() . Поскольку полный импульс сохраняется, находим скорости частиц в момент наибольшего сближения:
. Поскольку полный импульс сохраняется, находим скорости частиц в момент наибольшего сближения:
|
|
(2.42) |
Теперь применим закон сохранения энергии. В начальный момент, когда частицы находятся бесконечно далеко друг от друга, полная энергия ![]() складывается из их кинетических энергий:
складывается из их кинетических энергий:
|
|
(2.43) |
В момент наибольшего сближения полная энергия равна сумме кинетических энергий частиц и потенциальной энергии кулоновского взаимодействия между ними:
|
|
(2.44) |
Приравнивая правые части равенств (2.43) и (2.44) и подставляя выражение (2.42) для скорости ![]() , получаем в итоге соотношение
, получаем в итоге соотношение
|
|
(2.45) |
Здесь 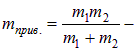 приведенная масса сталкивающихся частиц,
приведенная масса сталкивающихся частиц, ![]() относительная скорость частиц,
относительная скорость частиц, ![]() кинетическая энергия их относительного движения. Из (2.45) для
кинетическая энергия их относительного движения. Из (2.45) для ![]() получаем:
получаем:
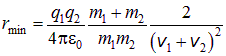
Эту формулу можно теперь применять к различным частным случаям. Например, если массы частиц одинаковы ![]() , то из (2.45) находим
, то из (2.45) находим
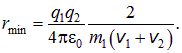
Если же масса второй частицы гораздо больше массы первой ![]() , то минимальное расстояние получается в два раза меньшим, чем при равенстве масс:
, то минимальное расстояние получается в два раза меньшим, чем при равенстве масс: