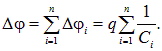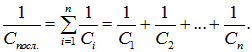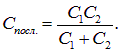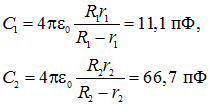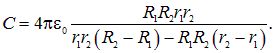2.6. Соединения конденсаторов

Последовательное соединение

Во многих случаях для получения нужной электроемкости конденсаторы объединяют в группу, которая называется батареей. Емкость батареи конденсаторов зависит от схемы соединения составляющих ее конденсаторов. Различают два вида соединения: последовательное и параллельное. Возможен также и смешанный тип соединения конденсаторов в батарею.

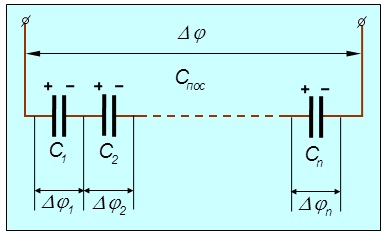
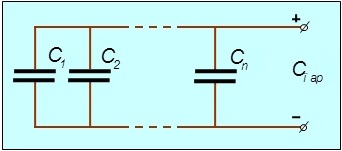
Рис. 2.13. Последовательное соединение конденсаторов Последовательное соединение. При зарядке батареи (рис. 2.13) разность потенциалов распределится между отдельными конденсаторами и будет равна   (2.19) Если первой обкладке батареи конденсаторов сообщается заряд , то на ее второй обкладке появится индуцированный заряд . Поскольку эта обкладка соединена с первой обкладкой второго конденсатора и поскольку действует закон сохранения заряда, на последней появится заряд . В свою очередь, это приведет к появлению заряда  на другой обкладке второго конденсатора и т. д. В результате все последовательно соединенные конденсаторы будут заряжены одинаково, причем батарее мы сообщили только заряд . Разности потенциалов  ,   и т. д.  могут быть не равны между собой, так как емкости отдельных конденсаторов, вообще говоря, неодинаковы. Поэтому разность потенциалов на клеммах всей батареи находится как сумма напряжений   на каждом из конденсаторов:   (2.20) С другой стороны,   (2.21) где емкость всей батареи. 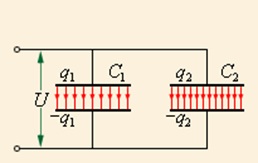Следовательно, емкость батареи последовательно соединенных конденсаторов определяется выражением:   (2.22) Для батареи из двух конденсаторов, например, отсюда следует выражение (рис. 2.14)     (2.23)

 

Параллельное соединение

Рис. 2.15. Параллельное соединение конденсаторов  При параллельном соединении конденсаторов (рис. 2.15) разность потенциалов батареи равна разности потенциалов каждого отдельного конденсатора: (2.24) Заряжая такую батарею, мы сообщаем ей заряд, часть которого попадет на обкладки первого конденсатора, часть — на обкладки второго и т. д. Вследствие закона сохранения электрического заряда полный заряд батареи параллельно соединенных конденсаторов будет равен сумме зарядов отдельных конденсаторов:   (2.25) Для каждого конденсатора можно написать соотношение   (2.26) подставляя которое в (2.25), получим:   (2.27) С другой стороны,   (2.28) где   емкость всей батареи. Сравнивая (2.27) и (2.28) окончательно получаем   (2.29) то есть при параллельном соединении конденсаторов емкость батареи равна сумме емкостей отдельных конденсаторов. Для батареи из двух конденсаторов, например, отсюда следует выражение (рис. 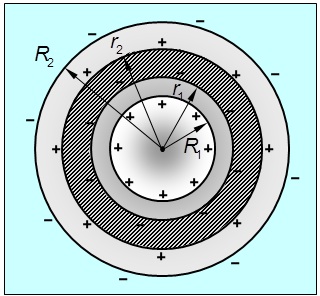2.16)    Рис. 2.16. Параллельное соединение двух конденсаторов  Задача. В сферический конденсатор с радиусами   см внутренней сферы и   см внешней сферы поместили сплошную сферическую проводящую оболочку с внутренним   см и внешним   см радиусами (рис. 2.17).  Сравнить емкости прежнего и нового конденсаторов.    Рис. 2.17. Сферический конденсатор с проводящей оболочкой внутри можно предста­вить как последовательное соединение двух сферических конденсаторов (к задаче 2.38.)

Решение. Емкость  прежнего конденсатора, чьими обкладками были сферы  радиусами    дается  формулой (2.18):

 

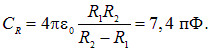
Как видно из рисунка, новый конденсатор представляет собой после­довательное соединение двух сферических конденсаторов: образованного сферами радиусами  (его емкость обозначим как ) и  (его емкость будет ). Имеем по той же формуле:

(2.30)

Для емкости   последовательно соединенных конденсаторов получаем теперь

 

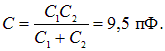
Емкость нового конденсатора оказалась больше емкости первоначального.

Аналитическая формула для емкости такой батареи имеет вид: 

(2.31)

 При бесконечно тонкой внутренней сфере  заряды на ее поверхностях скомпенсируют друг друга, и мы должны получить формулу для емкости конденсатора  без внутренней оболочки. Так оно и следует из формулы (2.31) при . В обратном предельном случае, когда стенки внутренней оболочки близки к обкладкам первоначального конденсатора, получается формула для емкости двух последовательно со­единенных плоских конденсаторов.

Конденсаторы нашли широкое практическое применение, особенно в радиотехнике. Некоторые типы конденсаторов показаны на рис. 2.18.

Рис. 2.18. Различные типы конденсаторов, применяемых в технике: 1 —  конденсаторы постоянной емкости; 2 — конденсатор переменной емкости

  

Дополнительная информация

http://www.elektropolus.com/condensator/type.php — типы конденсаторов;

http://gete.ru/post_1212414212.html — классификация и маркировка конденсаторов;

http://www.chipdip.ru/video.aspx?vid=ID000274696&tag=dielectric   — видео «Конструкция электролитического алюминиевого конденсатора»;

http://www.symmetron.ru/articles/tantalum_replacement.shtml — керамические конденсаторы большой емкости;

http://radiobooka.ru/radio_nach/kak_sdelat_kondensator.phtml — как сделать конденсатор своими руками;

http://chipinfo.ru/literature/radio/194701/p54-57.html  — статья «Переменные конденсаторы»;

http://www.eham.net/articles/5217  — переменный конденсатор своими руками;

http://www.kpsec.freeuk.com/components/capac.htm — коденсаторы, переменные конденсаторы;

http://qrx.narod.ru/arhn/e_d.htm  — бесконтактные емкостные датчики;

http://www.lionprecision.com/capacitive-sensors/index.html   — обзор емкостных датчиков;

http://pda-reader.ru/93  — принципы работы сенсорных экранов;

http://pcavto.ru/kak-eto-rabotaet/printscipyi-rabotyi-sensornyix-ekranov-touch-screen.html — как работают сенсорные экраны разных типов.