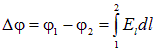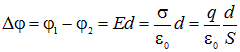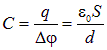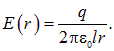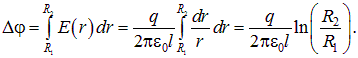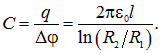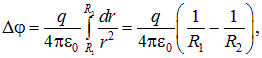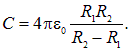2.5. Конденсаторы

Повышения емкости проводника можно достигнуть не только увеличением его размеров, но и за счет приближения к нему другого проводника. Примерами могут служить плоский конденсатор, сферический конденсатор и др. Мы вычислим их емкости, исходя из данных определений и геометрии конденсатора.

Плоский конденсатор (рис. 2.11). 

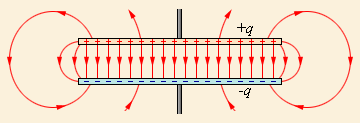
Рис. 2.12.  Электрическое поле идеального плоского конденсатора

Идеальный плоский конденсатор предста­вляет собой две металлические параллельные пластины, линейные размеры которых много больше расстояния  между ними. Пусть площадь каждой из пластин равна  (рис. 2.12). На одну пластину помещен заряд , на другую —  Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь «краевыми» эффектами — распределениями зарядов и конфигурациями полей вблизи их краев.

Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью. Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:

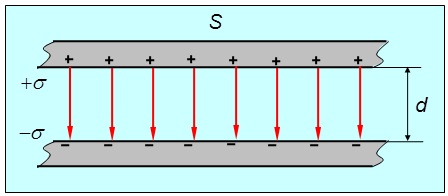
Рис. 2.12.  Электрическое поле идеального плоского конденсатора

Видео 2.9. Геометрия реального плоского конденсатора и распределение заряда на его пластинах.

Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью . Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними: 

(2.10)

Поле, создаваемое двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями, является одно­родным, и его напряженность равна   (см. (2.3)).

Напряженность поля в пространстве, окружающем пластины, можно считать равной нулю, если пренебречь краевыми эффектами. Интегрируя вдоль силовой линии (которые ортогональны пластинам), получаем

(2.11)

Отсюда находим емкость плоского конденсатора:

(2.12)

Цилиндрический конденсатор. Цилиндрический конденсатор представляет собой два коаксиальных длинных проводящих цилиндра радиусами  и  и длиной . Предполагая, что , мы и в этом случае пренебрегаем краевыми эффектами. Линейная плотность заряда на цилиндрах равна . Мы уже вывели выражение для электрического поля длинного заряженного цилиндра (см. (1.17)):

(2.13)

Электрическое поле направлено по радиусу цилиндров. Интегрируя по этому пути от одной обкладки к другой, находим разность потенциалов между обкладками:

(2.14)

Отсюда следует выражение для емкости цилиндрического конденсатора:

(2.15)

В случае, когда зазор между обкладками  , можно использовать первый член разложения логарифма в ряд Тейлора

 

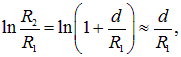
что приводит к выражению

(2.16)

В скобках стоит произведение длины окружности цилиндра на его высоту, что равно площади поверхности цилиндра (площади обкладок). Т. о. мы воспроизвели в этом пределе выражение (2.12) для емкости плоского конденсатора.

Сферический конденсатор. Сферический конденсатор образуется двумя концентрическими сферами радиусам  и . Интегрируя вдоль радиуса уже хорошо знакомое выражение

 

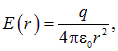
получаем разность потенциалов между обкладками:

(2.17)

откуда

(2.18)

Если внешний радиус бесконечно велик  (физически  это значит, что ), то вычитаемым в знаменателе можно пренебречь, и мы приходим к формуле (2.9) для емкости уединенной сферы. В обратном случае, когда зазор между обкладками  можно положить в числителе  Замечая, что  есть площадь обкладок, мы снова приходим к формуле (2.12).

Видео 2.10. Влияние диэлектрика на распределение зарядов на проводнике и его емкость.

Задача. Конденсатор, используемый в чипе запоминающего устрой­ства компьютера, имеет емкость  и заряжается до разности потенциалов . Каково число  избыточных электронов на его отрицательной обкладке? В какой массе воды полное число всех атомных электронов равно ?

Решение. Заряд конденсатора равен . Чтобы найти число избыточных электронов, надо разделить  на заряд электрона:  Почти два миллиона электронов, много это или мало? Для этого найдем массу воды с тем же числом электро­нов. Молекула воды  содержит два атома  и один атом , то есть всего 10 электронов. Стало быть, в интересующей нас массе воды должно содержаться молекул. Число молекул в одном моле равно  то есть надо взять моля. Молярный вес воды равен  кг/кмоль, так что искомая масса составляет кг, то есть крайне мала.   Миллион частиц — много в мире электронов, но совсем мало в масштабах нашего мира.