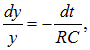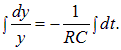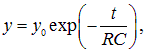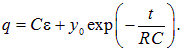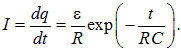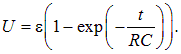4.4. Зарядка конденсатора

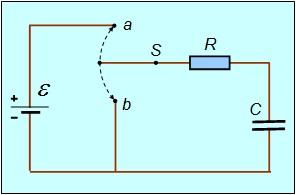
В этом разделе мы решим задачи о зарядке и разрядке конденсатора. Электрическая цепь показана на рис. 4.20. Переключатель S позволяет подсоединять и отсоединять источник тока.

Рис. 4.20. Цепь для зарядки и разрядки конденсатора

Пусть сначала конденсатор емкостью С не заряжен, и мы перебрасываем выключатель в положение а. По цепи пойдет зависящий от времени ток I(t), переносящий положительный заряд на верхнюю пластину конденсатора. Отметим, что хотя ток зарядки и разрядки конденсатора не является постоянным, но рассматривается здесь, поскольку его изменение в данном случае можно считать медленным. Обозначим заряд на этой пластине в момент t через q(t). Напряжение на конденсаторе можно найти как разницу между ЭДС и падением напряжения на нагрузке, то есть либо как отношение заряда к емкости q/C. Приравнивая эти выражения, получаем первое уравнение процесса зарядки

(4.36)

Согласно закону сохранения заряда, изменение заряда q на обкладках конденсатора происходит только из-за наличия тока I. Поэтому второе уравнение процесса имеет вид

(4.37)

Подставим (4.37) в (4.36):

(4.38)

Мы видим, что у этого уравнения имеется стационарное решение (постоянный заряд на конденсаторе)

При таком заряде на конденсаторе напряжение на нем равно ЭДС источника тока, и ток по цепи не идет

Введем отклонение у заряда на конденсаторе от его стационарного значения

или

Подставляя это соотношение в (4.38), находим уравнение для функции y(t)

Это уравнение легко интегрируется

откуда

Вычисляя интегралы. находим

или

где y₀ — произвольная постоянная интегрирования (значение у в начальный момент времени). Отсюда находим заряд на конденсаторе

Нам осталось использовать начальное условие: в момент t = 0 конденсатор был не заряжен

Отсюда находим

и окончательно

(4.39)

Дифференцируя q(t) по времени, находим ток в цепи

(4.40)

Напряжение на конденсаторе U(t) = q(t)/C без труда получается из (4.39)

(4.41)

Таким образом, по мере роста заряда и напряжения на конденсаторе ток в цепи уменьшается. При этом заряд конденсатора стремится к своему стационарному значению а напряжение на конденсаторе — к ЭДС источника тока. Величина имеет размерность времени и определяет характерное время процесса зарядки. За промежуток ток в цепи уменьшается
в е = 2,72 раза.

На рис. 4.21 показана зависимость заряда на конденсаторе и тока в цепи для конкретных значений R = 1,5 кОм, С = 2 мкФ, Характерное время процесса равно при этих значениях Из рисунков видно, что уже при временах порядка

конденсатор почти полностью заряжается.

Рис. 4.21. Графики зависимости напряжения на конденсаторе (слева) и тока в цепи (справа)
при зарядке конденсатора емкостью С = 2 мкФ через активное сопротивление R = 1,5 кОм от источника тока с ЭДС 12 В

Рассмотрим теперь процесс разрядки конденсатора. Зарядив его до какого-то заряда (или, что то же самое, до начального напряжения U₀ = q₀/C), мы перебрасываем переключатель в положение b (см. рис. 4.20). Конденсатор начнет разряжаться, а по цепи пойдет ток. Мы имеем те же самые уравнения за исключением того, что в цепь не включен источник тока. Поэтому в этом случае надо положить в уравнении (4.38). Тогда оно совпадет с тем, что мы ранее решали для y(t), поэтому решения для процесса разрядки конденсатора нам уже известны

(4.42)

Все эти величины быстро уменьшаются с течением времени: за тот же характерный промежуток заряд конденсатора, напряжение на нем и ток в цепи падают в 2,72 раза. Отрицательный знак в выражении для тока означает, что ток при разрядке течет в направлении, обратном току при зарядке конденсатора.

Дополнительная информация

http://www.scorcher.ru/art/electronica/electronica1.php — зарядка — разрядка конденсатора.

5/9