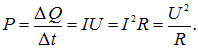4.6. Закон Джоуля — Ленца

Предположим, что на концах участка проводника имеется разность потенциалов  Перемещаясь из точки 2 с большим потенциалом в точку 1, где потенциал меньше, положительный заряд  теряет энергию

По определению для постоянного тока

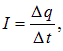
тогда

и теряемая энергия (или работа сил электрического поля) равна

 

Куда же девается эта энергия? Она не переходит в кинетическую энергию заряда, так как при постоянном токе дрейфовая скорость зарядов неизменна. Вспомним, что заряд не ускоряется из-за столкновений с атомами кристаллической решетки проводника. Значит, если в проводнике течет ток и проводник неподвижен, то работа сил электрического поля расходуется на нагревание проводника. Сталкиваясь с частицами проводника, носитель заряда передает им свою энергию, которую получает от поля. Поэтому работа поля над зарядами переходит, в конечном счете, в энергию теплового (хаотического) движения атомов проводника, то есть происходит нагревание проводника (рис. 27, 28, 29).

Видео 4.4. Нагревание металлического проводника током: плавкий предохранитель.

Рис. 4.27. Выделение теплоты в электрическом разряде

Видео 4.5. Искровой разряд в воздухе.

Рис. 4.28. Выделение теплоты в сопротивлении и лампе накаливания

Видео 4.6. Дуговой разряд в воздухе.

Рис. 4.29. Выделение теплоты в нагревательном элементе 

Видео 4.7. Выделение тепла в последовательно соединенных проводниках с разным удельным сопротивлением.

Таким образом, работа А, произведенная за время выделяется в проводнике в виде теплоты

Данная формула носит название закона Джоуля — Ленца. Закон установлен Дж. Джоулем в 1841 г. (рис. 4.30) и независимо от него русским физиком Э.X. Ленцем в 1842 г. 

Рис. 4.30. Д. Джоуль (1818–1889) — английский физик

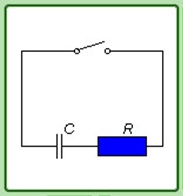
 Пример. Пусть конденсатор емкостью С, заряженный до разности потенциалов U, разряжается через сопротивление R. Найти полное количество теплоты, выделившееся на нагрузке (рис. 4.31). 

 

Рис. 4.31. Электрическая цепь с заряженным конденсатором и сопротивлением 

Решение. В (4.42) мы нашли ток разрядки как функцию времени. Подставляем его в (4.57) и интегрируем по t.

Как и следовало ожидать, в теплоту перешла вся энергия электрического поля, запасенная первоначально в конденсаторе.  

Количество теплоты, выделяемой в единицу времени (то есть тепловая мощность Р), равно

Тепло выделяется по всему объему проводника. Найдем плотность тепловой мощности, то есть мощность, выделяемую в единице объема. Представим себе линейный проводник с постоянным сечением S  и длиной l. Тогда напряжение на концах проводника можно выразить через напряженность электрического поля в нем

С другой стороны, сопротивление проводника равно

(напомним, что — проводимость данного вещества, обратная его удельному сопротивлению ). Отсюда находим

Таким образом, плотность тепловой мощности равна

где j — плотность тока. Мы вывели эту формулу для линейного проводника, но она верна и в общем случае тоже. Для проводников сложной формы или составленных из разных материалов выделяемую в единицу времени теплоту можно подсчитать, интегрируя плотность тепловой мощности по всему объему проводника

 

На рис. 4.32 показан опыт, демонстрирующий распределение мощности между последовательно и параллельно соединенными проводниками с различным сопротивлением. Для этого в в цепь с напряжением 40 В включаются две лампы, мощности которых равны 25 Вт и 150 Вт при подаче на них напряжения, равного 127 В. При последовательном соединении этих ламп светится нить только лампы меньшей мощности, имеющей большее сопротивление, а при параллельном соединении сильнее накал лампы большей мощности, имеющей меньшее сопротивление. 

 

Рис. 4.32. Распределение мощности между последовательно и параллельно соединенными проводниками

 

Дополнительная информация

http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Kirchhoff.html  — Густав Роберт Кирхгоф (1824–1887);

http://www-history.mcs.st-and.ac.uk/Biographies/Kirchhoff.html — Густав Роберт Кирхгоф (1824–1887); 

https://www.msu.edu/~brennem2/joule/home.htm  — Джеймс Прескот Джоуль (1818–1889);

http://www.hrono.ru/biograf/bio_l/lenc_eh.php — Эмилий Христианович Ленц (1804–1865).