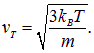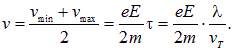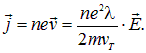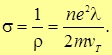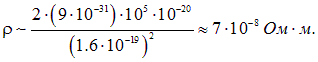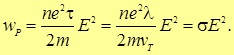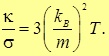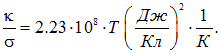4.7. Классическая теория

В начале двадцатого столетия был экспериментально доказан тот факт, что носителями тока в металлах являются свободные электроны. Исходя из этих представлений, немецкий физик Друде создал (1900 г.) классическую электронную теорию проводимости металлов, усовершенствованную затем другими физиками. Внутренняя структура металлов характеризуется кристаллической решеткой, например такой, какая изображена на (рис. 4.33).  

 

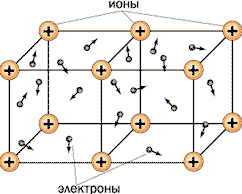
Рис. 4.33. Схема кристаллической решетки металлов 

В узлах решетки расположены положительные ионы, представляющие собой атомы металла, лишенные одного или нескольких валентных электронов и поэтому заряженные положительно. Эти положительные ионы способны совершать лишь небольшие тепловые колебания около своих положений равновесия в узлах кристаллической решетки. В пространстве между ионами практически свободно движутся оторвавшиеся от атомов и «обобществленные» кристаллом валентные электроны, образуя так называемый электронный газ. Согласно теории Друде, электроны в кристаллической решетке ведут себя во многом подобно идеальному газу, поэтому можно использовать для описания их поведения известные формулы кинетической теории газов (рис. 4.34). 

 

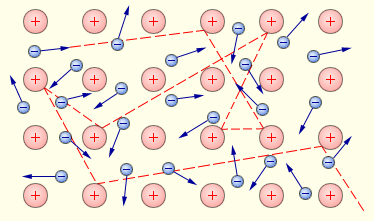
Рис. 4.34. Газ свободных электронов в кристаллической решетке металла.
Показана траектория одного из электронов 

В отсутствие внешнего поля любые направления скорости электронов, находящихся в хаотическом тепловом движении, равновероятны, следовательно, средняя плотность тока равна нулю, и можно сказать, что электронный газ в целом покоится по отношению к положительным ионам решетки. Согласно классической термодинамике, средняя энергия поступательного теплового движения молекул любого газа зависит лишь от температуры T, но не от химической природы и молекулярного веса газа и равна

Отсюда находим среднеквадратичную скорость хаотического движения частиц

Замечание: Отметим, что соотношения (4.62), (4.63) и вытекающие из них справедливы лишь тогда, когда распределение частиц (в данном случае электронов) по скоростям максвелловское, что, в свою очередь, имеет место тогда, когда поступательное движение полностью классично. Электронный газ в металле представляет собой квантовую систему и распределением Максвелла не описывается. Поэтому предпринятое ниже изложение классической теории Друде представляет ограниченный интерес, как способ получения качественно (по размерности) правильных соотношений, которые никак не могут претендовать на количественное согласие с экспериментом.

Мы видели (см. п. 4.1), что для комнатных температур v_Т = 10⁶ м/с. При наличии внешнего электрического поля электроны в металле будут также обладать некоторой средней (дрейфовой) скоростью v направленного движения против внешнего поля Е. Согласно данным выше оценкам, скорость v на много порядков меньше скорости v_Т (рис. 4.35).  

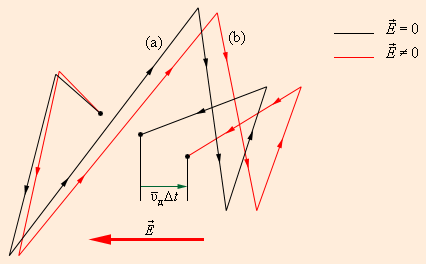
Рис. 4.35. Движение свободного электрона в кристаллической решетке:
а — хаотическое движение электрона в кристаллической решетке металла;
b — хаотическое движение с дрейфом, обусловленным электрическим полем.
Масштабы дрейфа сильно преувеличены

Если рассматривать электронный газ в металле как идеальный газ, то тепловое движение электронов в кристаллической решетке можно охарактеризовать средней длиной свободного пробега , то есть средним расстоянием, проходимым свободно движущимися электронами в металле между двумя последовательными столкновениями с ионами решетки. Среднее время между двумя столкновениями будет

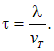
Так как v << v_Т, то можно считать, что ни  ни  не меняются при наложении электрического поля Е. 

Закон Ома

При наличии внешнего электрического поля Е на электрон действует сила F = еЕ, вследствие чего он приобретает ускорение

(m — масса электрона). Будем считать, что при столкновении с ионом электрон полностью теряет свою скорость направленного движения: v_min = 0. Далее он начинает ускоряться электрическим полем и к следующему столкновению приобретает скорость

Следовательно, средняя скорость направленного движения v за период между двумя столкновениями, то есть за время  составляет

Значит, плотность тока будет равна

Сопоставляя полученное для плотности тока j  выражение с законом Ома (4.9), получаем формулу для проводимости s  и для связанного с ним удельного сопротивления 

Приведем численные оценки. как будет показано в дальнейшем, связь длины свободного пробега с эффективным
сечением  рассеивающего центра (иона) и концентрацией этих центров имеет вид

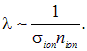
Для металлов, как мы уже обсуждали, концентрация ионов примерно совпадает с концентрацией свободных электронов

Подставляя выражение для    в формулу (4.66), получаем

Оценку для сечения  можно получить, зная порядок диаметров атомов

откуда

Скорость хаотического движения была оценена как v_Т = 10⁵ м/с. Получаем теперь из (4.67) значение удельного сопротивления

Полученная оценка действительно воспроизводит порядок величины удельных сопротивлений металлов, представленных в таблице (см. п. 4.3). 

Закон Джоуля — Ленца

При столкновении с ионом, как мы предположили, электрон передает ему набранную за время 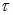 энергию дрейфа

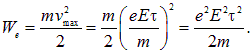
Умножая W_e  на концентрацию электронов n и деля на время  получаем тепловую энергию, передаваемую единице объема проводника в единицу времени (то есть плотность мощности)

Последнее равенство в этой цепочке получено с использованием выражения (14.66) для  . В результате мы вывели закон Джоуля — Ленца (4.60) из микроскопической теории.

 Закон Видемана — Франца 

Металлы, наряду с высокой электропроводностью, характеризуются также и большой теплопроводностью. В 1853 г. немецкие физики Г. Видеман и Р. Франц установили эмпирический закон, согласно которому отношение коэффициента теплопроводности k к коэффициенту электропроводности s для всех металлов приблизительно одинаково и изменяется пропорционально температуре. Теплопроводность металлов значительно превышает теплопроводность диэлектриков, из этого можно заключить, что теплопроводность в металлах в основном обусловлена электронным газом, а не его кристаллической решеткой. Для коэффициента теплопроводности электронного газа в металле можно заимствовать выражение из кинетической теории газов

где произведение nm концентрации электронов на их массу подставлено вместо плотности электронного газа. 

Удельная теплоемкость одноатомного газа равна

Подставляя это значение в выражение для коэффициента теплопроводности k, получим

Разделив k  на , получим

Поскольку

приходим к соотношению

Это соотношение выражает закон Видемана — Франца. Подставив значения k_В = 1,38·10^–23 Дж/К и е = 1,6·10^–19 Кл, получим

Однако полученное соотношение недостаточно точно согласуется с экспериментом, то есть классическая теория объяснила закон Видемана — Франца лишь качественно. Следующая из классической теории зависимость удельного сопротивления от температуры

также не согласуется с экспериментом. Объяснение всех несоответствий смогла дать только квантовая теория.