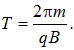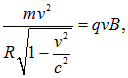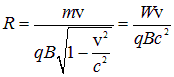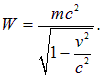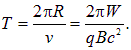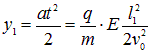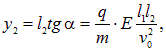5.4. Некоторые применения магнитного поля

Циклотрон

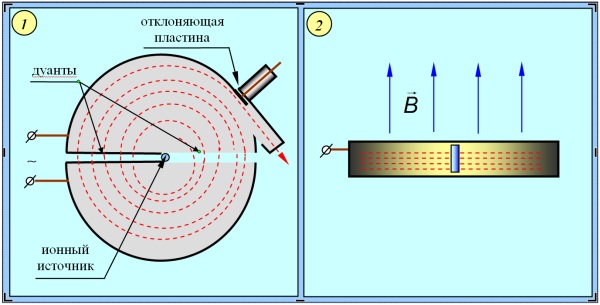
Независимость периода обращения нерелятивистской заряженной частицы в однородном магнитном поле от ее скорости положена в основу ускорителя заряженных частиц, называемого циклотроном. В циклотроне заряженная частица, помещенная между полюсами электромагнита, многократно проходит через электрическое поле, каждый раз увеличивая свою энергию на величину от нескольких сотен до нескольких тысяч электронвольт. С увеличением скорости частицы (с ростом ее энергии) радиус орбиты увеличивается, поэтому частица в циклотроне будет двигаться по спирали. Циклотрон состоит из двух электродов в виде половинок круглой невысокой коробки (рис. 5.16).

Рис. 5.16. Схема циклотрона: 1 — вид сверху; 2 — вид сбоку

Электроды называются дуантами из-за сходства их формы с заглавной латинской буквой D. Дуанты заключены в откачиваемый корпус (вакуум 10^–5 мм рт. ст.), который помещен между полюсами большого электромагнита. Поле, создаваемое электромагнитом, однородно и перпендикулярно к плоскости дуантов. На дуанты подается переменное напряжение, создаваемое высокочастотным генератором. Вблизи центра магнита в промежутке между дуантами располагается источник заряженных частиц — ионов. Положительный ион, вылетающий из источника в то время, когда электрод 2 имеет отрицательный потенциал, приобретает некоторую скорость и в внутри дуанта 2 опишет полуокружность постоянного радиуса, так как внутри дуанта электрическое поле отсутствует, но есть магнитное поле. К моменту выхода электрона из дуанта 2 при помощи высокочастотного генератора изменяется направление электрического поля на обратное: дуант 1 приобретает отрицательный потенциал, а дуант 2 положительный. Поэтому ион вновь ускорится и внутри дуанта 1 опишет полуокружность уже большего радиуса (но время прохождения полуокружности останется неизменным!). Двигаясь в резонансе с высокочастотным полем, ионы будут по спирали приближаться к краю магнита, причем их энергия будет расти после каждого прохождения частицей ускоряющего промежутка между дуантами. Пучок ускоренных ионов выходит из циклотрона с помощью отклоняющего электрода, на который подается высокий отрицательный потенциал.

На рис. 5.17 показаны циклические ускорители заряженных частиц.

Рис. 5.17. Циклические ускорители элементарных частиц:
1 — первый советский циклотрон (1935);
2 — современный циклотрон для исследований в области управляемого термоядерного синтеза

Циклотрон используется в качестве ускорителя тяжелых элементарных заряженных частиц и многозарядных положительных ионов. Имеются причины принципиального характера, которые ограничивают возможности значительного увеличения энергии ионов в циклотроне. Период обращения в циклотроне пропорционален массе частицы

Однако в ускорителях, где частицы разгоняются до скоростей, близких к скорости света, приходится учитывать релятивистское выражение для импульса частицы. Тогда уравнение движения будет иметь вид

откуда для радиуса орбиты получаем

Здесь мы использовали выражение для релятивистской энергии W частицы

Находим тогда для периода обращения

При малых кинетических энергиях

и мы возвращаемся к прежней формуле. Однако по мере ускорения частиц период обращения растет вместе с энергией, тогда как период высокочастотного поля в циклотроне не изменяется. В результате при каждом очередном попадании в ускоряющую щель частицы будут опаздывать, приобретая все меньшую энергию, пока не начнут попадать в тормозящее поле. Поэтому для достижения больших энергий частиц используется два приема:

с увеличением периода обращения частицы уменьшают частоту изменения потенциала дуантов. Ускорители, в которых используется этот принцип, называются фазотронами.
по мере роста энергии частицы увеличивают магнитное поле при неизменной частоте ускоряющего электрического поля. Действительно, если отношение E/В сохранить неизменным, то есть с ростом энергии частицы плавно увеличивать магнитную индукцию поля, то период обращения частицы тоже будет постоянным. На этом принципе работают синхротроны и синхрофазотроны.

Определение заряда и массы электрона

Уравнение движения (уравнение второго закона Ньютона) частицы массы с зарядом , движущейся в электромагнитном поле, имеет вид

(5.16)

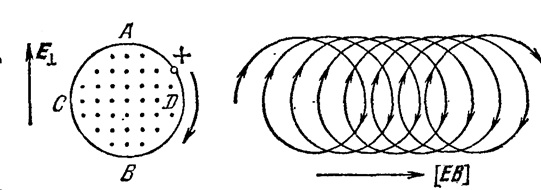
Видно, что при любой конфигурации полей заряд и масса входят в виде отношения — удельного заряда . Поэтому, измеряя параметры траектории заряженной частицы в электромагнитном поле можно определить именно её удельный заряд (рис. 5.18). Остается создать удобную для измерений конфигурацию электрического и магнитного полей.

Рис. 5.18. Траектория движения заряженной частицы в скрещенных электрическом и магнитном поле

Рассмотрим заряженную частицу, движущуюся в пространстве со скоростью и попадающую в перпендикулярное к направлению её движения однородное электрическое поле

причем область поля имеет протяженность l₁ (рис. 5.19).

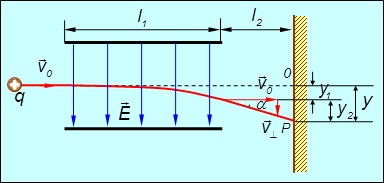
Рис. 5.19. Движение заряженной частицы в отклоняющем электрическом поле

В отсутствие поля частица попала бы в точку 0 на экране. На частицу же в поле действует сила F, направленная перпендикулярно скорости v₀, из-за чего частица приобретает ускорение а = (q/m)E, где q/m — удельный заряд частицы. За время пролета области поля

частица сместится по вертикали на расстояние

(5.17)

и приобретет составляющую скорости, перпендикулярную к направлению начальной скорости v₀

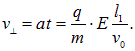
Далее частица, вылетевшая из области действия поля, движется свободно, имея скорость

направленную под углом к первоначальной, причем

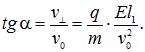
За время подлета к экрану частица успеет дополнительно сместиться на расстояние

(5.18)

(см. рис. 5.19). В конечном итоге она попадает в точку P экрана, отстоящую от точки 0 на расстояние

(5.19)

Полученные результаты позволяют сделать следующие выводы:

частицы с одинаковой скоростью и одинаковым удельным зарядом q/m отклоняются одинаково;
чем больше скорость частицы, тем меньше они отклоняются;
отклонение уменьшается с уменьшением удельного заряда частицы (то есть разные частицы будут попадать в различные точки экрана).

В 1897 г. Дж.Дж. Томсон впервые определил удельный заряд электрона е/m почти по такой схеме, использовав газоразрядную трубку (рис. 5.20). Электронный пучок проходил через отверстие в аноде и попадал в область однородного электрического поля конденсатора и перпендикулярного ему магнитного поля, создаваемого катушкой с током (на рис. 5.20 область магнитного поля показана пунктиром).

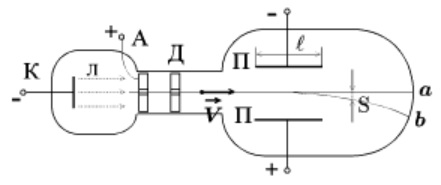
Рис. 5.20. Газоразрядная трубка, использовавшаяся для определения удельного заряда электрона

При выключении поля, пучок электронов, двигаясь в направлении начальной скорости v₀, создавал светящееся пятно в точке 0 флуоресцирующего экрана. Включение магнитного поля вызывало смещение светящегося пятна на экране. Затем, подбирая величину напряженности Е электрического поля конденсаторов, можно было добиться, чтобы пучок электронов не смещался относительно точки 0. В этом случае действие на электроны электрического и магнитного полей взаимно компенсировалось, то есть выполнялось условие (в (5.20) учтено, что )

(5.20)

Зная напряженности полей, можно было определить скорость электронов v₀ = E/B. Меняя поля и измеряя смещение светящегося пятна на экране, по скорости электронов и геометрическим размерам установки определяли удельный заряд электрона. Томсон получил

современное значение

Масс-спектрометры

Для определения удельного заряда широко используются также приборы, называемые масс-спектрометрами или масс-спектрографами. Различие в названии приборов связано с различным способом регистрации ионов: при помощи электронных схем (масс-спектрометры) или при помощи фотографических пластинок (масс-спектрографы).

Различные типы этих приборов основаны на использовании фокусирующих свойств электрических и магнитных полей по отношению к заряженным частицам. Заряженные частицы (ионы или ядра) ускоряются электрическим полем (рис. 5.21).

Рис. 5.21. Схема действия масс-спектрографа

После прохождения разности потенциалов U кинетическая энергия частиц равна

(5.21)

где q = Ze — заряд иона (или ядра), m — масса иона, v — его скорость. Попадая в вакуумную камеру с однородным магнитным полем с магнитной индукцией В, перпендикулярной начальной скорости, частицы описывают полукруг (под влиянием силы Лоренца). Радиус окружности, по которой движется ион в магнитном поле, находится из условия

(5.22)

Описав половину окружности, ионы попадают на фотопластинку на расстоянии 2R от щели. Решая совместно два уравнения — (5.21) и (5.22), получим

(5.23)

Следовательно, ионы каждого сорта (определяемые значением q/m) в зависимости от величины отклоняющего магнитного и ускоряющего электрического полей попадают на фотопластинку в некоторое определенное место, характеризуемое величиной радиуса R. Зная параметры прибора, величины B и U, можно найти удельные заряды ионов.

Дополнительная информация

http://nuclphys.sinp.msu.ru/spargalka/a16.htm — ускорители;

http://nuclphys.sinp.msu.ru/experiment/accelerators/ciclotron.htm — циклотрон;

http://www.aip.org/history/lawrence/first.htm — циклотрон, первый циклотрон;

http://nuclphys.sinp.msu.ru/experiment/accelerators/synchro.htm — синхротрон;

http://www1.jinr.ru/Books/veksler/35.pdf — статья «В.И. Векслер и начало исследований на синхрофазотроне»;

http://elementy.ru/lib/430461 — синхрофазотрон;

http://www.chemheritage.org/discover/chemistry-in-history/themes/atomic-and-nuclear-structure/thomson.aspx — Дж.Дж. Томсон (1856–1940);

http://nuclphys.sinp.msu.ru/enc/e046.htm — масс-спектрометр;

http://www.chemguide.co.uk/analysis/masspec/howitworks.html — как работает масс-спектрометр;

http://www.astbury.leeds.ac.uk/facil/MStut/mstutorial.htm — статья «Введение в масс-спектромтерию»;

http://www.slac.stanford.edu/ — стендфордская национальная ускорительная лаборатория (см. раздел virtual visitor center);

http://nuclphys.sinp.msu.ru/experiment/ — учебное пособие «Частицы и ядра» МГУ;

http://lhc.web.cern.ch/lhc/ — Большой Адронный Коллайдер (LHC);

http://www-bdnew.fnal.gov/tevatron/ — теватрон в Национальной ускарительной лаборатории Ферми;

http://uspas.fnal.gov/ — школа ускорителей и физики частиц США;

http://www.ihep.ru/ — институт физики высоких энергий в Протвино;

http://www.vitart.ru/kapitsa/1-1-Strong_magnetic_fields.html — статья П.Л. Капицы «Сильные магнитные поля, их получение и эксперименты с ними»;

http://www.valtar.ru/Magnets3/magnets4.htm — получение магнитных полей;

http://ufn.ru/ufn29/ufn29_1/Russian/r291c.pdf — статья «Получение магнитных полей и работы П.Л. Капицы».

5/8