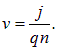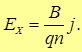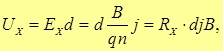5.5. Эффект Холла

В 1880 г. Э. Холл обнаружил, что в проводнике, помещенном в магнитное поле, возникает разность потенциалов в направлении, перпендикулярном вектору магнитной индукции B и току I. Объясняется это действием силы Лоренца на заряды, движущиеся в проводнике.

 На рисунке 5.22 изображена пластина из проводника, которую пронизывает магнитное поле с индукцией B, направленное перпендикулярно чертежу от нас (обозначено крестиком).

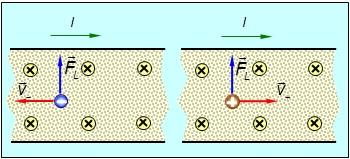
Рис. 5.22. При фиксированном направлении тока сила Лоренца,
действующая на носители зарядов в образце, помещенном в магнитное поле,
имеет одно и то же направление независимо от знака заряда носителя

У отрицательных зарядов вектор скорости v и ток I направлены в противоположные стороны, для положительных зарядов направления скорости и тока совпадают. Применяя правило винта, находим, что сила Лоренца в обоих случаях направлена к верхней грани пластины. Следовательно, носители зарядов, независимо от знака их заряда, накапливаются на верхней грани пластины. 

Эффект Холла наблюдается у металлов и полупроводников. У металлов и полупроводников n-типа, где носителями зарядов являются электроны, на верхней грани пластины скапливаются избыточные отрицательные заряды, а нижняя грань заряжается положительно (рис. 5.23). У полупроводников p-типа, где носителями являются так называемые дырки, имеющие положительный заряд, верхняя грань заряжается положительно, а нижняя — отрицательно.

 

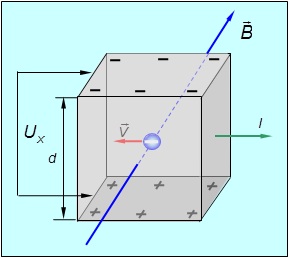
Рис. 5.23. Эффект Холла заключается в возникновении разности потенциалов U_Х ,
между гранями проводящей пластины с током, помещенной в магнитное поле
(знаки зарядов показаны для металлической пластины)

Так как

то сила Лоренца равна

(5.24)

Заряды, скопившиеся на верхней и нижней границах пластины, создают электрическое поле напряженностью E_X , которое в свою очередь воздействует на электрические заряды с силой

(5.25)

Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, эти две силы уравновешивают друг друга

то есть

откуда

(5.26)

Заметим, что здесь автоматически выполняется соотношение между скоростью зарядов и полями E_X и B, с которым мы только что познакомились, обсуждая опыты Томсона по измерению удельного заряда электрона. При выполнении соотношения (5.26) заряд движется прямолинейно и равномерно в скрещенных электрическом и магнитном полях. 

Из формулы для величины плотности тока j = qnv находим скорость упорядоченного движения зарядов

(5.27)

Таким образом, для напряженности поперечного (холловского) электрического поля получаем

Следовательно, при расстоянии между гранями пластины d разность потенциалов между ними равна

где R_X = 1/qn — коэффициент пропорциональности, называемый постоянной Холла. Плотность носителей зарядов (электронов) в металле n = 10²⁸ м^–3, откуда R_X = 10^–9 м³/Кл. Для наиболее распространенных полупроводников
R_X = 0,1 м³/Кл.  

Эффект Холла — один из эффективных методов изучения свойств носителей зарядов в металлах и полупроводниках. На рис. 5.24 представлен опыт, в котором демонстрируется возникновение поперечной ЭДС при внесении полупроводника с током в магнитное поле, перпендикулярное току. Плоский полупроводниковый образец, закрепленный на держателе, вносится в поле постоянного магнита, и вольтметр фиксирует наличие ЭДС Холла. При переворачивании образца относительно поля знак ЭДС меняется на противоположный.

Рис. 5.24. Эффект Холла в полупроводнике 

 

Дополнительная информация 

http://electrik.info/main/fakty/97-yeffekt-xolla-i-datchiki-na-ego-osnove.html — эффект Холла и датчики на его основе;

http://www.explainthatstuff.com/hall-effect-sensors.html — эффект Холла,  практические применения;

http://www.radioland.net.ua/contentid-170-page1.html — Полупроводники p и n типа.