5.6. Закон Ампера
Теперь мы готовы к обсуждению взаимодействия тока с магнитным полем.
Ампер установил наличие силового взаимодействия между двумя проводниками, по которым текут электрические токи. Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
Рис. 5.25. Опыт Ампера по исследованию взаимодействия параллельных токов:
1 — схема установки; 2 — отталкивание антипараллельных токов; 3 — притяжение параллельных токов
Если по ним пропускать токи, текущие в противоположных направлениях, то проводники будут отталкиваться друг от друга (см. рис. 5.25-2). Если же токи будут течь в одном направлении, то они будут притягиваться (см. рис. 5.25-3).
Видео 5.4. Взаимодействие параллельных токов.
Эксперименты, проведенные Ампером, показали, что на проводник с током, помещенный в магнитное поле, действует сила. Откуда же она берется? Обсуждая эффект Холла, мы видели, что сила электрического поля EХ уравновешивает силу Лоренца, действующую на электроны. Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl · S. В силу нейтральности проводника в целом таков же по абсолютной величине и полный заряд ионов кристаллической решетки. Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
|
|
(5.30) |
где мы выразили плотность тока через его силу
Обращаем внимание, что в эту формулу не вошли характеристики конкретных носителей заряда, но лишь полный ток через проводник.
У нас внешнее магнитное поле было ортогонально току. В общем случае направление тока будем характеризовать вектором dl, имеющем длину dl и направленным вдоль течения тока. В холловскую напряженность электрического поля дает вклад только компонента магнитного поля, ортогональная вектору dl. Эта компонента равна по величине
где 
есть угол между векторами B и dl. Тогда для величины силы имеем
|
|
(5.31) |
Учитывая направление этой силы (правило винта), можем записать ее в векторной форме
|
|
(5.32) |
Выражение (5.32) носит название закона Ампера, а сила 
называется силой Ампера (рис. 5.26).
Рис. 5.26. Сила Ампера, действующая на провод с током в поле постоянного магнита
Видео 5.5. Сила Ампера: выпрыгивание провода из магнита.
Мы получили выражение для силы, действующей на элемент проводника dl. Для определения полной силы, действующей на проводник, надо проинтегрировать (5.32) вдоль его длины, учитывая зависимость магнитного поля от положения элемента. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле
|
|
(5.33) |
Направление силы Ампера определяется по правилу левой руки (рис. 5.27):
|
Если левую руку расположить таким образом, чтобы линии магнитной индукции входили в ладонь, а вытянутые пальцы были направлены в направлении тока, то отогнутый большой палец покажет направление действия силы Ампера, действующей на проводник. |
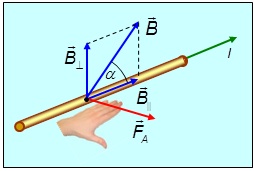
Рис. 5.27. Определение направления силы Ампера
Видео 5.6. Сила Ампера: тележка Эйхенвальда.
Действие силы Ампера на проводник с током демонстрируется в опыте, показанном на рис. 5.28. На торце вертикальной цилиндрической катушки положены горизонтальные проводящие рельсы, по которым может катиться алюминиевая трубка. После включения тока через катушку к рельсам прикладывается постоянное напряжение, и по трубке начинает течь ток. Под действием силы Ампера трубка катится по рельсам. При изменении направления тока в трубке она катится в противоположную сторону.
Рис. 5.28. Экспериментальное изучение силы Ампера
В общем случае произвольного проводника и магнитного поля силы, действующие на различные элементы проводника, различаются как величиной, так и направлением (рис. 5.29).
Рис. 5.29. В общем случае силы, действующие на различные элементы проводника,
различаются как величиной, так и направлением
С помощью формулы (5.31) можно определить величину магнитной индукции по максимальной силе Ампера dFA (в этом случае 
), действующей на элемент dl проводника с током I
То есть величина магнитной индукции численно равна максимальной силе, действующей на единичный элемент тока.
