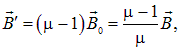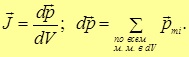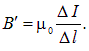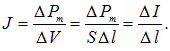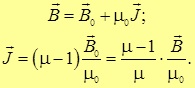7.1. Магнетики
В присутствии магнетика вектор магнитной индукции ![]() равен сумме векторов магнитной индукции внешнего магнитного поля
равен сумме векторов магнитной индукции внешнего магнитного поля ![]() , создаваемого независимыми от магнетика токами, и магнитной индукции собственного поля магнетика
, создаваемого независимыми от магнетика токами, и магнитной индукции собственного поля магнетика ![]()
|
|
(7.1) |
Поле ![]() , создаваемое намагниченным магнетиком, разумеется, зависит от того, как намагничен магнетик, а намагничивается он суммарным полем
, создаваемое намагниченным магнетиком, разумеется, зависит от того, как намагничен магнетик, а намагничивается он суммарным полем ![]() , поэтому
, поэтому ![]() само является функцией
само является функцией ![]() :
: ![]() . Исключением в этом смысле может быть постоянный магнит, намагниченность которого не зависит, или практически не зависит от наличия или отсутствия внешнего магнитного поля, в частности, такое вещество, которое может оставаться намагниченным и в отсутствие внешнего — намагничивающего — поля.
. Исключением в этом смысле может быть постоянный магнит, намагниченность которого не зависит, или практически не зависит от наличия или отсутствия внешнего магнитного поля, в частности, такое вещество, которое может оставаться намагниченным и в отсутствие внешнего — намагничивающего — поля.
Далее будет показано, что если магнитное поле вне магнетика параллельно его поверхности, то поле ![]() связано с магнитной индукцией
связано с магнитной индукцией ![]() в вакууме (то есть в отсутствие магнетика) соотношением
в вакууме (то есть в отсутствие магнетика) соотношением
![]()
Безразмерная величина m называется магнитной проницаемостью. Все магнетики, в зависимости от характера влияния их собственного поля на суммарное магнитное поле, можно разделить на три группы:
-
парамагнетики, у которых m > 1, то есть вектор магнитной индукции собственного магнитного поля
 направлен в ту же сторону, что и вектор внешнего магнитного поля
направлен в ту же сторону, что и вектор внешнего магнитного поля 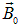 ;
; -
диамагнетики, у которых m < 1, то есть векторы
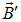 и
и 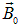 направлены в противоположные стороны;
направлены в противоположные стороны; -
ферромагнетики, это парамагнетики, у которых m >> 1.
В парамагнитных телах собственное поле ![]() увеличивает магнитный поток и, следовательно, парамагнитные тела притягиваются к магниту. В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита.
увеличивает магнитный поток и, следовательно, парамагнитные тела притягиваются к магниту. В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита.
Видео 7.1. Поведение пара- и диамагнетиков в неоднородном магнитном поле.
Как показывает опыт, вектор магнитной индукции собственного поля пара- и диамагнетика пропорционален вектору магнитной индукции внешнего поля B0
Безразмерный коэффициент пропорциональности cm называется магнитной восприимчивостью вещества и является безразмерной величиной. У диамагнитных веществ магнитная восприимчивость является отрицательной величиной (cm < 0), у парамагнитных положительной (cm > 0). У ферромагнетиков магнитная восприимчивость cm зависит от величины магнитной индукции внешнего поля B0, поэтому в общем случае зависимость собственного поля ферромагнетика от внешнего нельзя считать линейной.
Результирующее магнитное поле в присутствии магнетика равно:
Сравнивая (7.3) с (7.1), получим
Отсюда находим связь собственного поля с внешним
аналогичную соответствующим выражениям для диэлектриков.
Для объяснения намагничивания тел Ампер предположил, что в атомах и молекулах вещества циркулируют особые круговые токи — молекулярные токи. Каждый такой ток создает в окружающем пространстве магнитное поле. В силу хаотической ориентации магнитных моментов отдельных молекулярных токов суммарный магнитный момент тела равен нулю. Под действием внешнего магнитного поля магнитные моменты молекулярных токов приобретают преимущественную ориентацию в одном направлении, вследствие чего вещество намагничивается — его суммарный магнитный момент становится отличным от нуля, возникает дополнительное поле ![]() (рис. 7.1).
(рис. 7.1).
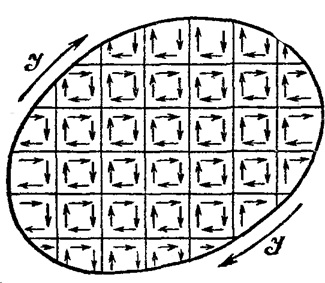
Рис. 7.1. Молекулярные токи в магнетике
Не вдаваясь пока в обсуждение природы молекулярных токов, получим соотношения, аналогичные тем, что были выведены для диэлектриков. Каждый молекулярный ток имеет магнитный момент ![]() . Намагничение (Степень намагниченности) магнетика естественно охарактеризовать магнитным моментом единицы объема, называемого вектором намагничивания (или намагниченностъю).
. Намагничение (Степень намагниченности) магнетика естественно охарактеризовать магнитным моментом единицы объема, называемого вектором намагничивания (или намагниченностъю).
Здесь ![]() — элементарный (физически бесконечно малый) объем магнетика, взятый в окрестности некоторой точки,
— элементарный (физически бесконечно малый) объем магнетика, взятый в окрестности некоторой точки, ![]() — магнитные моменты отдельных молекулярных токов. В формуле (7.6) суммируются магнитные моменты всех молекулярных токов, находящихся внутри объема
— магнитные моменты отдельных молекулярных токов. В формуле (7.6) суммируются магнитные моменты всех молекулярных токов, находящихся внутри объема ![]() .
.
|
В СИ единицей измерения вектора намагничивания является ампер на метр (А/м):
|
Поляризуемость диэлектрика (плотность электрического дипольного момента) связывалась с возникновением поверхностных зарядов, которые изменяли электрическое поле в среде. Аналогично этому, намагниченность магнетика приводит к возникновению поверхностных токов, что меняет магнитное поле. На рис. 7.2 показан образец магнетика, помещенный во внешнее магнитное поле ![]() .
.
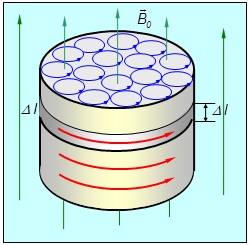
Рис. 7.2. Молекулярные токи в магнетике, помещенном в магнитном поле,
создают собственное поле, подобное полю соленоида с током I
Молекулярные токи, показанные на торце образца, ориентированы так, что их магнитные моменты выстроились параллельно вектору ![]() . Видно, что токи в толще магнетика компенсируют друг друга. Нескомпенсированными оказываются только токи вблизи поверхности образца. Складываясь, они приводят к поверхностным токам (показаны красными стрелками на рис. 7.2 и черными стрелками на рис. 7.3).
. Видно, что токи в толще магнетика компенсируют друг друга. Нескомпенсированными оказываются только токи вблизи поверхности образца. Складываясь, они приводят к поверхностным токам (показаны красными стрелками на рис. 7.2 и черными стрелками на рис. 7.3).
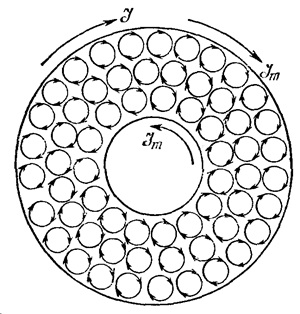
Рис. 7.3. Образование молекулярных токов на поверхностях магнетика
Такая система эквивалентна соленоиду. В формуле для магнитной индукции поля соленоида
![]()
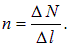
С другой стороны, произведение ![]() сть полный ток через элемент длиной
сть полный ток через элемент длиной ![]() . Поэтому формула для соленоида применима к нашему магнетику, если заменить произведение nI на линейную плотность поверхностного тока
. Поэтому формула для соленоида применима к нашему магнетику, если заменить произведение nI на линейную плотность поверхностного тока ![]() . Получаем тогда следующее выражение для величины магнитной индукции поля В ', создаваемого молекулярными токами
. Получаем тогда следующее выражение для величины магнитной индукции поля В ', создаваемого молекулярными токами
С другой стороны, магнитный момент элемента поверхностного тока, текущего по участку соленоида длиной ![]() , равен
, равен
где S — поперечное сечение образца. По определению вектора намагничивания
Сравнивая (7.7) и (7.9), находим связь вектора намагниченности с полем, создаваемым молекулярными токами
С учетом (7.1) и (7.5) можем записать
|
|
(7.11) |
Дополнительная информация
http://www.xumuk.ru/encyklopedia/2/3189.html — парамагнетики;
http://periodictable.com/Properties/A/MagneticType.html — магнитные материалы, парамагнетики, диамагнетики;
http://www.ndt-ed.org/EducationResources/CommunityCollege/MagParticle/Physics/MagneticMatls.htm — диамагнитные, парамагнитные и ферромагнитные материалы;
http://physics-animations.com/Physics/English/mag_txt.htm — ферромагнетики.