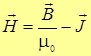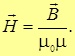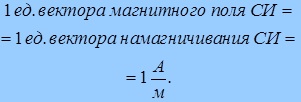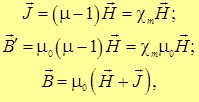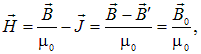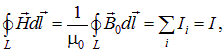7.2. Напряженность магнитного поля

В диэлектриках, помимо силовой характеристики электрического поля Е, мы ввели также вспомогательную величину — вектор электрического смещения

В наиболее распространенном случае линейной зависимости поляризованности изотропного диэлектрика от напряженности поляризующего поля имело место соотношение

 

Для магнетиков аналогичным образом также вводится вспомогательная величина — напряженность магнитного поля Н

обратите внимание на разные знаки, с которыми входят Р для диэлектриков и вектор J для магнетиков). С учетом полученных выше соотношений имеем

так что

Подчеркнем, что аналогом вектора напряженности электрического поля  является именно вектор магнитной индукции , а векторы  и  играют вспомогательную роль. Следует избегать ложных иллюзий, вызванных исторически закрепившимся названием «напряженность» магнитного поля для вектора . В терминах  полученные соотношения принимают вид

где  — магнитная восприимчивость магнетика.  

Мы видели, что циркуляция магнитной индукции в вакууме определялась током, пронизывающим выбранный контур L

 

Аналогичное выражение, естественно, справедливо и для циркуляции вектора   в веществе, но циркуляция собственного поля магнетика

 

приведет к появлению в правой части суммы молекулярных токов, которые нам не известны. Это крайне неудобно. Положение спасает введенный вектор напряженности магнитного поля Н. Из определения (7.12) и соотношения (7.10) следует

так что циркуляция вектора напряженности магнитного поля определяется только макроскопическими токами в системе

где I — полный макроскопический ток через контур L. Его можно выразить через плотность тока  через любую поверхность S, натянутую на контур L 

где dS = ndS, а вектор  — единичный нормальный вектор к элементарной площадке площадью dS. 

Для иллюстрации применения полученных формул вычислим магнитную индукцию в соленоиде с линейной плотностью витков n и силой тока I, если витки намотаны на сердечник с магнитной проницаемостью m. Найдем циркуляцию вектора напряженности магнитного поля Н  по тому же контуру, что и прежде (см. рис. 6.18). Ответ нам, в сущности, известен

 

(ср. с (6.34)). Контур охватывает тот же суммарный ток nlI, и (7.16) приводит к равенству

Используя теперь связь В = m₀mH, получаем выражение для магнитной индукции поля соленоида, заполненного магнетиком