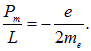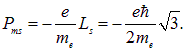7.3. Происхождение молекулярных токов
Электрон, движущийся в атоме по круговой орбите, можно условно уподобить контуру с током, и считать, что электрон образует круговой ток, сила которого I = en, где (–е) — заряд электрона, n — число оборотов электрона в секунду. Следовательно, магнитный момент такого контура равен
где r — радиус электронной орбиты.
Поскольку произведение длины окружности 
на частоту вращения n есть линейная скорость движения электрона на орбите
то
и
Эта величина называется орбитальным магнитным моментом электрона. Направление вектора 
образует с направлением тока (то есть с направлением движения положительных зарядов) правовинтовую систему. Движущийся по орбите электрон обладает моментом импульса
где mе — масса электрона. Вектор L называют орбитальным моментом импульса электрона. Он также образует с направлением движения электрона правовинтовую систему. Следовательно, для отрицательно заряженногого электрона направления векторов 
и 
противоположны.
Отношение магнитного момента элементарной частицы к ее моменту импульса называется гиромагнитным (магнитомеханическим) отношением. Для электрона оно равно
Кроме орбитального момента импульса электрон обладает собственным моментом импульса 
и соответствующим собственным магнитным моментом 
, для которых гиромагнитное (магнитомеханическое) отношение в два раза больше
Собственный механический момент (спин) и связанный с ним собственный (спиновый) магнитный момент являются неотъемлемыми свойствами электрона, как его масса и заряд. Аналогичная картина имеет место и для других элементарных частиц. Природа спина будет обсуждена при изучении основ квантовой механики. Отметим только, что в очень грубом приближении его можно связать с вращением частицы вокруг собственной оси (от англ. spin — верчение).
Спин элементарных частиц пропорционален фундаментальной постоянной — так называемой постоянной Планка
и выражается через неё следующим образом
где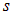 
— так называемое «спиновое квантовое число», принимающее значения
.
У электронов, протонов, нейтронов и ряда других элементарных частиц определяющее спин квантовое число 
. У мезонов 
, у фотона 
, у предполагаемого кванта гравитационного поля «гравитона» это квантовое число должно быть равно 
. Квантовое число, определяющее спин, как и сам спин, является одной из характеристик элементарных частиц наряду с массой и зарядом.
Таким образом, собственный момент импульса — спин — электронов, протонов и нейтронов равен
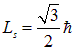
Ввиду однозначной связи между квантовым числом 
и спином 
общепринято говорить «спин», а называть соответствующее ему квантовое число, к недоразумениям это не приводит, то есть общепринято говорить, что спин электрона равен половине или 1/2. Согласно (7.22), собственный магнитный момент электрона равен
|
|
|
Величину
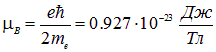
называют магнетоном Бора.
Как показывается в квантовой механике, орбитальный момент импульса выражается через соответствующее ему квантовое число так же, как и собственный момент импульса (спин)
|
(7.23) |
Важно то, что орбитальное квантовое число 
может принимать только целочисленные значения.
Как видно из (7.21) и (7.23), наименьший отличный от нуля орбитальный магнитный момент равен магнетону Бора:
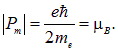
Результирующий магнитный момент атома образуется в результате векторного сложения (по правилам квантовой механики!) магнитных моментов всех элементарных частиц, содержащихся в атоме. Картина еще более усложняется при рассмотрении совокупностей молекул и атомов.
Дополнительная информация
http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Planck.html — Макс Планк (1858–1947).
