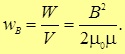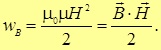8.4. Энергия магнитного поля

Обратимся снова к процессу замыкания цепи на рис. 8.33-1. Умножая правую и левую части уравнения (8.23) на , получим

Левая часть уравнения (8.29) выражает работу, совершаемую источником тока за время . В правой части первое слагаемое есть величина работы, расходуемой на выделение джоулева тепла в проводнике. Ясно, что перед нами — уравнение закона сохранения энергии в рассматриваемой цепи. Каков же смысл второго слагаемого? Оно связано с катушкой, о чем свидетельствует множитель L, и представляет собой работу, затраченную на преодоление противодействия ЭДС самоиндукции. Куда же девается эта работа? В процессе замыкания цепи в катушкой создается магнитное поле. Значит, указанная работа аккумулируется именно в катушке как запасенная в ней энергия её магнитного поля. Ток возрастает от нуля до некого установившегося значения I. Поэтому полная энергия поля катушки равна 

Поскольку

этот же результат можно записать в формах

Эти формулы очень похожи на выражения для энергии конденсатора как функции его заряда или разности потенциалов на обкладках. Мы помним, что их можно привести к виду, где явно выделен объем конденсатора. Это позволило нам связать плотность энергии электрического поля с его напряженностью. Выполним аналогичную программу и для магнитного поля, используя в качестве «катушки» достаточно длинный соленоид. 

Индуктивность соленоида дается выражением (8.21)

Магнитная индукция в соленоиде определяется по формуле (7.18)

Выразим плотность числа витков в соленоиде через магнитное поле в нем

и подставим в выражение для индуктивности соленоида. Получим

Наконец, подставим это выражение в формулу (17.28) для энергии поля в катушке 

Мы достигли своей цели: параметры соленоида, с которого мы начали, не присутствуют в этой формуле. Мы все выразили через магнитную индукцию поля, и энергия в катушке оказалась пропорциональной ее объему. Отсюда следует выражение для плотности энергии магнитного поля (неважно, чем и как созданного)

Вспоминая связь напряженности магнитного поля с магнитной индукцией

находим эквивалентные представления для плотности энергии магнитного поля:

Для магнитного поля в вакууме следует положить во всех этих формулах . Нетрудно заметить сходство (8.34) с аналогичными формулами (3.35), (3.36) для электрического поля (рис. 8.36, рис. 8.37).

Рис. 8.36. Мощное магнитное поле Солнца производит выбросы плазмы

Рис. 8.37. Мощное магнитное поле нейтронной звезды 

Пример. Сравнить энергии, содержащиеся в объеме 1 л, если он пронизан: 1) однородным электрическим полем с напряженностью Е = 100 кВ/м; 2) однородным магнитным полем с индукцией В = 1 Тл.

Решение. Энергия электрического поля равна

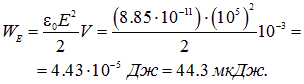
Энергия магнитного поля равна

Оба указанных поля считаются достаточно сильными, но могут быть созданы без особых проблем. Задача демонстрирует, что практически выгоднее накапливать энергию в магнитном поле: в данном примере отношение энергий равно