Приложение
Энергия магнитного поля системы контуров с токами
Энергия магнитного поля системы контуров с токами требует знания теоремы Стокса, формулы Остроградского — Гаусса и уравнений Максвелла. При первом чтении можно пропустить
Используем известное выражение для энергии магнитного поля
|
(П1) |
Здесь 
и 
— индукция и напряженность магнитного поля, причем 
. Предполагается, что магнитная проницаемость не зависит от 
, т. е. среда не ферромагнитна. Интегрирование ведется по всему объему, занимаемому магнитным полем. Нас будет интересовать энергия всей системы (контуров с током), поэтому объем предполагается достаточно большим, чтобы на его поверхности магнитное поле отсутствовало. Выразим скалярное произведение через векторный потенциал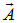 
. Используя связь магнитного поля и векторного потенциала, 
, а также основные формулы векторного анализа, получим:
При интегрировании по всему объему второе слагаемое исчезает. Действительно:
|
(П2) |
Последнее равенство справедливо, поскольку интегрирование ведется по поверхности, охватывающей всю область, занятую магнитным полем. Как уже говорилось, H = 0 на этой поверхности. Далее воспользуемся уравнением Максвелла
|
(П3) |
которое справедливо в отсутствии электрических полей. Подставляя (П3), (П2) в (П1), получим
Это общее выражение, при его выводе не делались предположения о форме плотности тока проводимости j. Пусть теперь эта плотность тока создается контурами с токами Ii
Тогда 
только в областях, занятых тонкими проводами. Выбрав линейный элемент провода 
с поперечным сечением 
, можно записать
Здесь учтено, что все три вектора сонаправлены. Тогда, поскольку это равенство верно для всех контуров со своими
токами 
, получаем выражение для энергии «n» контуров с током в виде
Интегрирование ведется по всем объемам Vi , в которых плотность тока отлична от нуля.
Используя теорему Стокса для векторного потенциала 
получаем окончательное выражение для энергии магнитного поля
|
(П4) |
Здесь Fi — поток вектора магнитной индукции через поверхность, охватываемую i-тым контуром тока. Он создается магнитными полями всех контуров с токами.
В основном тексте связь коэффициентов взаимной индуктивности получена на основе формулы (П4).
