8.7. Взаимная индукция в присутствии ферромагнетиков

Известно, что в присутствии ферромагнетиков правило (8) может не выполняться. Тем не менее, и в этом случае возможно выполнение подобного равенства. Проиллюстрируем равенство (1) на конкретном примере тороидального сердечника, сделанного из ферромагнетика. Приведем распространенную ситуацию, когда на сердечник намотаны два контура с различным числом витков. Магнитное поле, создаваемое токами, протекающими по обоим контурам, практически полностью сосредоточено в ферромагнетике.

Если в контуре «1» течёт ток , то в контуре «2» потокосцепление есть

Аналогично, при протекании в контуре «2» тока  возникает магнитный поток (потокосцепление), пронизывающий контур «1»

Здесь  и  — коэффициенты взаимной индукции.

По первой обмотке течёт ток , который порождает магнитное поле H₁, величина которого легко вычисляется по теореме о циркуляции

 

Здесь C — замкнутый путь длины l, проходящий внутри ферромагнетика. Поток магнитной индукции, проходящий через сечение сердечника, легко находится

 

Следовательно, потокосцепление через контур «2»:

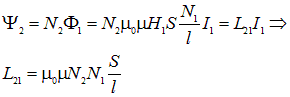
Мы получили выражение для коэффициентов взаимной индукции, симметричное относительно индексов 1 и 2. Поэтому очевидно, что аналогичные рассуждения для второго контура приведут к тому же результату и, значит, к выполнению равенства коэффициентов взаимной индукции.