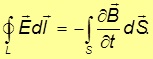9.1. Вихревое электрическое поле

Итак, давайте зафиксируем то, что мы уже успели изучить. Все наши формулы могут быть выведены из нескольких утверждений. 

Утверждение 1.  

Математической формулировкой этого утверждения является теорема Остроградского — Гаусса для напряженности электрического поля

В правой части стоит интеграл от плотности зарядов по произвольному объему, который равен полному заряду внутри него. В левой части — поток вектора напряженности электрического поля через произвольную замкнутую поверхность, ограничивающую этот объем. Как мы видели, закон Кулона также содержится в этом уравнении. 

Утверждение 2.  

Математической формулировкой этого утверждения является теорема Остроградского — Гаусса для вектора магнитной индукции, в правой части которой стоит нуль

Утверждение 3. 

Математически это выражается как равенство нулю циркуляции напряжённости электростатического поля по произвольному контуру

Утверждение 4.  

Математическим выражением этого утверждения является теорема о циркуляции вектора магнитной индукции

В левой части стоит циркуляция магнитного поля по произвольному контуру L, а в правой — интеграл от плотности полного тока по произвольной поверхности S, натянутой на этот контур. Этот интеграл равен сумме токов, пересекающих поверхность S. В этом уравнении содержится закон Био — Савара — Лапласа. 

Эти четыре уравнения надо дополнить выражением для силы Лоренца, действующей на движущиеся заряды со стороны электромагнитных полей

Внимательный читатель заметит, что заголовки к двум последним утверждениям выделены другим шрифтом. Это сделано не случайно: данные утверждения подлежат модификации. Дело в том, что с тех пор, как мы сформулировали эти четыре утверждения, мы познакомились еще с одним явлением — электромагнитной индукцией. Оно пока еще не нашло отражения в выписанных уравнениях. Сделаем это. 

Если магнитный поток через проводящий виток L меняется, то в витке возникает ЭДС индукции. Что это означает? Заряды, находящиеся в проводнике, будут испытывать действие силы, связанной с этой ЭДС. Но появление силы, действующей на заряд, означает появление какого-то электрического поля. Циркуляция этого поля по витку как раз и равна по определению ЭДС индукции

Отличие циркуляции от нуля означает, что данное электрическое поле не потенциально, а имеет вихревой характер, подобно магнитному полю. Но если такое поле появилось, то в чем тогда роль витка? Виток — это не более, чем удобный детектор для регистрации вихревого электрического поля по возникшему индукционному току. Для того, чтобы расстаться с витком окончательно, выразим ЭДС индукции через поток магнитного поля. Перепишем закон Фарадея в виде

Объединяя это уравнение с (9.6), приходим к модифицированному утверждению 3 (рис. 9.1). 

Утверждение 5.  

 

Рис. 9.1. Закон электромагнитной индукции в трактовке Максвелла:
изменяющееся магнитное поле порождает вихревое электрическое поле 

Математически это выражается в виде уравнения

В этом уравнении содержится закон электромагнитной индукции Фарадея. 

Здесь надо проявить немного осторожности: раз у нас появилось дополнительное электрическое поле, не изменит ли оно первое утверждение? По счастью, ответ отрицателен: поток вихревого поля через замкнутую поверхность равен нулю, так что это поле не даст вклада в левую часть уравнения (9.1). 

Казалось бы, мы учли уже все явления, с которыми знакомы. Почему же тогда мы пометили четвертое уравнение как требующее модификации? Дело в том, что теперь нарушена симметрия между электрическими и магнитными явлениями. Предположим, что в системе нет ни зарядов, ни токов. Может ли существовать тогда электромагнитное поле? Ответ мы знаем из современной жизни: может! Существуют же электромагнитные волны, которые распространяются в космосе и не требует для этого никакой среды. В отсутствие зарядов и токов первые два уравнения (9.1) и (9.2) вполне симметричны. Этого нельзя сказать о второй паре уравнений. Электрическое (вихревое) поле можно породить без зарядов, просто изменением магнитного поля? Почему же магнитное поле нельзя породить не токами, а изменяя электрическое поле?