1.4. Распределение энергии по степеням свободы молекулы

Чтобы разобраться в связи температуры с внутренней энергией, повторим введенное ранее в механике понятие — число степеней свободы.

В § 1.3 было показано, что давление газа численно равно импульсу, который передается за единицу времени единице площади стенки в результате ударов по ней молекул, поэтому давление определяется средней энергией только поступательного движения молекул.

Поступательное движение любой системы «как целого» полностью определяется движением одной единственной точки: её центра масс. В частности, полный импульс  любой нерелятивистской системы, равен произведению массы  этой системы на скорость  движения её центра масс. Энергия поступательного движения системы «как целого» равна . Поэтому, для полного описания поступательного движения любой системы в трехмерном пространстве необходимо и достаточно задание значений трех координат центра масс. Таким образом, поступательному движению, как бы ни была устроена система, всегда соответствуют  три поступательных степени свободы: .

Можно сказать и так: «с точки зрения поступательного движения» любая система может быть точно, а не приближенно, представлена в виде одной единственной материальной точки совпадающей с центром масс системы и имеющей массу равную массе системы (рис. 1.15).

Рис. 1.15. Одноатомная молекула

Если же говорить о полной внутренней энергии газа U, то она складывается, вообще говоря, из многих компонентов, соответствующих всем возможным видам движения в молекуле и энергии взаимодействия молекул между собой. При рассмотрении идеального газа, энергией взаимодействия молекул пренебрегают.

Рассмотрим для начала благородный газ, например, гелий . Дело в том, что все благородные газы одноатомны, из них гелий самый легкий и, соответственно, самого простого устройства. Атом гелия (имеется в виду основной изотоп ) — это положительно заряженное ядро из 2 протонов и 2 нейтронов и электронная оболочка из 2 отрицательно заряженных электронов. Итого 6 частиц, если каждую из них считать материальной точкой, то это 18 степеней свободы. Но, не все так удручающе мрачно, выручает квантовая механика. Не вдаваясь в «квантовые» подробности, укажем, что для изменения состояния электронной оболочки атома гелия, а именно: для перевода её из основного состояния с минимально возможной энергией в имеющее большую энергию возбужденное состояние необходима минимальная энергия около 20 эВ. Более точно, например, при возбуждении электронной оболочки атома гелия возможен переход, требующий 19,8198 эВ. Энергетический спектр атомов дискретен: принять меньшую энергию атом гелия просто не может, он так устроен. При столкновении атома гелия с электроном меньшей энергии, атом гелия останется в исходном — основном состоянии с наименьшей возможной внутренней энергией, величина которой зависит только от выбора начала отсчета энергии, и, чаще всего, принимается просто равной нулю. Такое столкновение будет абсолютно упругим. Отметим, что

Поэтому энергии в 20 эВ соответствует температура порядка  кельвинов. Наверное нетрудно сообразить, что даже при температуре в К атомов гелия движущихся столь быстро, что энергия их относительного движения в 100 раз больше её среднего значения, будет ничтожно мало. Но, тогда столкновения, сопровождающиеся изменением внутренней энергии одного из сталкивающихся атомов, будут чрезвычайно редки, следовательно, возможным наличием атомов с возбужденной электронной оболочкой можно пренебречь и приближенно считать, что все атомы имеют электронную оболочку в одном и том же основном состоянии с минимально возможной энергией. Не так важно, что электронные оболочки всех атомов имеют минимально возможную энергию, как важно, что она одна и та же у всех атомов и не меняется даже при сильном нагреве газа. Тогда, суммарная энергия электронных оболочек всех атомов есть просто константа равна 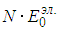, где N — число атомов в газе, а 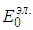— энергия электронной оболочки каждого из атомов. При фиксированном полном числе атомов эта величина ни от каких параметров состояния газа не зависит. Остается ещё раз вспомнить, что энергия всегда определена с точностью до аддитивной постоянной и выбросить эту константу, изменив начало отсчета энергии.

Для изменения состояния ядер атомов необходима энергия в сотни тысяч эВ, что «по газовым масштабам» чудовищно много. Соответствующие температуры наблюдаются лишь во внутренних областях Звёзд. Поэтому о возможности изменения внутреннего состояния ядер в процессе столкновений в газе говорить не приходится (имеются ввиду стабильные ядра, возможный распад нестабильных ядер не имеет отношения к параметрам состояния газа).

Что же остается? Остается поступательное движение атома как целого, то есть три поступательных степени свободы. Это оправдывает использование такой модели:

На всякий случай оговоримся, что в данный момент нас не интересуют процессы установления в газе термодинамического равновесия. Равновесие устанавливается именно в результате взаимодействия частиц газа при их столкновениях, поэтому модель «атом — материальная точка» такие процессы не описывает.

Положение с электронной оболочкой не меняется, если атомы входят в состав многоатомной молекулы. Минимальная энергия, необходимая для изменения состояния (возбуждения) электронной оболочки молекул примерно та же, что и для возбуждения электронных оболочек атомов. Характерная для атомно-молекулярного мира цифра составляет порядка 10 эВ, чему соответствует температура порядка сотни тысяч кельвинов. При таких температурах газ уже не газ, а низкотемпературная плазма. Поэтому, пока газ остается газом, в подавляющем большинстве случаев, можно с великолепной точностью считать, что электронные оболочки всех молекул газа находятся в одном и том же состоянии, их суммарная энергия есть не зависящая от параметров состояния газа константа, которую можно опустить. Конечно есть исключения, требующие известной осторожности. Например, у молекулы кислорода  есть — по атомно-молекулярным меркам — весьма долгоживущее возбужденное состояние, для перевода в которое этой молекуле требуется всего 0,982 эВ. Именно в этом состоянии молекула кислорода чрезвычайно активна химически, это весьма важное и интересное своими последствиями исключение, но исключение, которое совершенно необходимо учитывать в соответствующих задачах, например, при расчетах скоростей химических реакций с участием этой молекулы.

Таким образом, и в составе молекулы, атом можно рассматривать как материальную точку.

Отдельно остановимся на подсчете числа вращательных и колебательных степеней свободы многоатомных молекул. Начнем с рассмотрения вращательных степеней свободы двухатомной молекулы. Все двухатомные молекулы линейны по той простой причине, что две несовпадающих точки определяют прямую, другими словами, две точки всегда лежат на одной прямой (рис. 1.16). Есть и более сложные, но линейные молекулы, например, молекула углекислого газа  линейна: в основном (с наименьшей возможной энергией) состоянии все три её атома лежат на одной прямой.

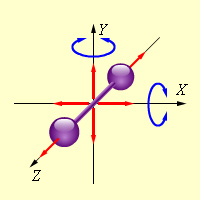
Рис. 1.16. Двухатомная молекула

Обычно, при расчете внутренней энергии газа, учитывается вращение линейной молекулы только вокруг двух её главных осей, проходящих через центр масс и перпендикулярных оси молекулы, вращение молекулы вокруг её оси симметрии не рассматривается,  что совершенно правильно. Но на этом основании заявляется, что у линейной молекулы только 2 вращательных степени свободы, что категорически неправильно. Впрочем, дальше и мы будем так писать, что, разумеется, требует объяснений. То, что вращательных степеней свободы только две, очевидным образом неправильно по следующей причине. Линейная молекула это пространственное образование, имеющее конечные размеры во всех трех измерениях. Например, расстояние между ядрами  в молекуле  составляет метра, а газокинетический радиус  (радиус в модели: молекула — шарик) равен  метра. Радиусы ядер азота порядка  метра. Учитывая, что , возникает законный вопрос: «Почему бы ей не вертеться и вокруг собственной оси?» Опять "виновата" квантовая механика. Квантовомеханический расчет показывает, что энергия, необходимая для того чтобы возбудить вращение вокруг некоторой оси, обратно пропорциональна моменту инерции относительно этой оси. Поэтому, о возбуждении вращения ядер речь не идет — слишком мал радиус этих «шариков», соответственно, слишком велика минимальная энергия необходимая для приведения их во вращательное движение. Это опять сотни килоэлектронвольт: так называемые, вращательные уровни энергии ядер. Остается одно: «завертеть» вокруг оси молекулы её электронную оболочку, но всякое изменение состояния электронной оболочки требует энергии порядка 10 эВ. Конкретно, чтобы «завертеть» молекулу  вокруг её оси, то есть перевести молекулу  в первое  вращательно-возбужденное состояние, требуется 7,35 эВ, чему соответствует температура, превышающая семьдесят тысяч градусов. Таким образом, при «газовых» температурах, то есть при тех температурах, когда газ ещё газ, а не плазма (меньших нескольких тысяч градусов) число линейных молекул вращающихся вокруг собственной оси будет пренебрежимо мало.

Рис. 1.17. Линейная молекула

Общая ситуация такова. Кажущееся отсутствие у молекулы некоторых степеней свободы есть следствие того, что энергия, необходимая для возбуждения соответствующих видов движения, в силу квантовых причин, слишком велика (а не мала!, рис. 1.17). Молекул, в которых эти виды движения возбуждены в результате столкновений молекул между собой, либо нет вовсе (в разумных количествах газа),  либо они есть, но в настолько малом относительном количестве, что вклад во внутреннюю энергию газа этих видов движения пренебрежимо мал. Это касается всех тех степеней свободы, которые связаны с электронами электронной оболочки молекулы. Именно по этой причине и изолированный атом и атом в молекуле можно рассматривать как материальную точку (рис. 1.18).

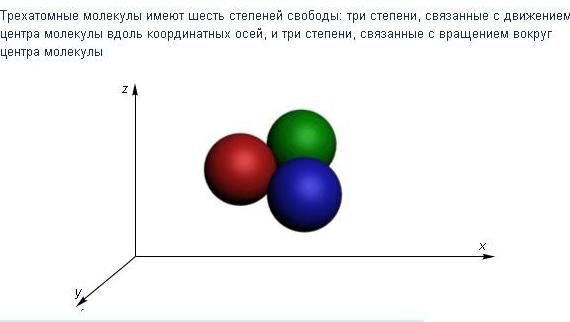
Рис. 1.18. Трехатомная молекула

В силу сказанного, определение числа степеней свободы молекулы в рамках модели: «атом — материальная точка», сводится к следующему.

Если молекула состоит из  атомов — материальных точек, степеней свободы:

всего — , из них:

поступательных — 3 всегда,

вращательных — 3 (пространственная молекула) или 2 (линейная молекула),

колебательных —   или для пространственной (линейной) молекул.

Настоятельно рекомендуем подсчитывать степени свободы именно в таком порядке: всего, поступательных, вращательных, что осталось – колебательные. Не следует ориентироваться на структурные химические формулы, на них показаны химические связи, а не возможности тех или иных колебательных движений групп ядер или отдельных ядер входящих в состав молекулы атомов. Например, никак не отражается возможность крутильных колебаний. Использование этих формул чаще всего приводит к ошибкам при подсчете числа колебательных степеней свободы. О структуре молекулы необходимо знать только одно: линейная она или нет.

Приведем три примера подсчета числа степеней свободы для молекул . Предварительно введем «число  классическое», которое обозначим так , оно потребуется в дальнейшем:

,

здесь  число поступательных степеней свободы,  число вращательных степеней свободы и  число колебательных степеней свободы. Из-за двойки перед  это число вовсе не равно полному числу степеней свободы молекулы и не должно так называться.

Таблица 1.4.1.

Молекула / Степеней свободы;	линейная	плоская	линейная	плоская или пространственная
Всего	6	9	9	24
Поступательных	3	3	3	3
Вращательных	2	3	2	3
Колебательных	1	3	4	18
Число	7	12	13	42

 Молекула этана имеет две равновесные конфигурации: в одном случае все восемь атомов лежат в одной плоскости, в другой равновесной конфигурации плоскости, в которых лежат «левая» четверка  и «правая» четверка , взаимно перпендикулярны. В обеих равновесных конфигурациях возможны крутильные колебания этих плоскостей с атомами около своих положений равновесия. Колебания атомов, а точнее ядер атомов, входящих в состав многоатомной молекулы, суть внутреннее движение в молекуле, поэтому удобнее всего рассматривать это движение в системе центра масс молекулы.

Чтобы понять, почему у трехатомной молекулы воды три колебательных степени свободы, а у также трехатомной молекулы углекислого газа их четыре, рассмотрим собственные моды колебаний ядер в молекуле  .

Четыре моды колебаний этой молекулы представляют собой следующее. Симметричная мода: все три ядра остаются на одной прямой, ядро углерода неподвижно, два ядра кислорода колеблются в противофазе, то есть половину периода они сближаются друг с другом и с ядром углерода, двигаясь к нему с двух противоположных сторон; другую половину периода они, по-прежнему в противофазе, удаляются друг от друга и от ядра углерода. Асимметричная мода: все три ядра остаются на одной прямой, два ядра кислорода, как единое целое (при неизменном расстоянии между ними) колеблются в противофазе с ядром углерода. Двукратно вырожденная деформационная мода: ядра не остаются на одной прямой; в тот момент, когда они покидают положения равновесия, находящиеся на прямой  , они (все три) движутся в направлениях перпендикулярных к этой прямой. Если, условно говоря, ось молекулы горизонтальна и ядро углерода движется вверх, то оба ядра кислорода движутся при этом вниз. То есть, два ядра кислорода колеблются синфазно между собой и в противофазе с ядром углерода. Это понятно: иначе центр масс молекулы не будет оставаться неподвижным.

Две строго равные собственные частоты двукратно вырожденной деформационной моды соответствуют движению ядер в двух взаимно перпендикулярных плоскостях. Если возбуждены колебания только одной из двух деформационных мод, то все три ядра остаются в фиксированной в пространстве плоскости. Если возбуждены колебания в обеих взаимно перпендикулярных плоскостях (обе моды), то траектории всех трех ядер, как результат сложения двух взаимно перпендикулярных колебаний со строго равными астотами, есть эллипсы, а при равных амплитудах и сдвиге по фазе  — окружности. При этом, если ядро углерода движется по своему эллипсу «по» часовой стрелке, то оба ядра кислорода движутся по своим одинаковым эллипсам «против часовой стрелки». Слова «по» и «против» взяты в кавычки по очевидной причине: они условны, так как зависят от того, с какой стороны смотреть.

Таким образом, четырем колебательным степеням свободы молекулы  соответствуют только три разных частоты, так как деформационная мода двукратно вырождена.

У любой двухатомной молекулы в рамках модели «атом — материальная точка» есть одна колебательная степень свободы, которой соответствует весьма простое движение: осциллирует расстояние между двумя её ядрами. Однако, нередко, макроскопические характеристики двухатомного газа, например, его теплоемкости при постоянном объеме  и давлении , их отношение — показатель адиабаты  и другие, имеют (с процентной точностью!) такие значения, как если бы у этих молекул колебательной степени свободы не было. Подчеркнем, что этот «казус» имеет место, во-первых, не для всех молекул и, во-вторых, лишь при не слишком больших температурах, не превышающих нескольких сотен кельвинов. Такая ситуация имеет место, например, для воздуха (грубо 80 % азота  и 20 % кислорода ) при комнатных температурах . Совершенно очевидно, что число степеней свободы молекулы не может зависеть от параметров состояния газа, в состав которого она входит. Это число определяется трехмерностью пространства и моделью: «атом — материальная точка». Спрашивается: «В чем дело?».

Для возбуждения колебаний ядер в молекуле азота ей  необходимо сообщить энергию не меньшую, чем , у молекулы кислорода, как говорят в таких случаях, «колебательный квант»  немного меньше, а именно: . Предваряя сам квантовомеханический расчет, сообщим его результаты.

При комнатной температуре доля колебательно-возбужденных молекул азота от их общего числа составит примерно 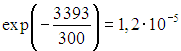, для кислорода эта доля примерно равна 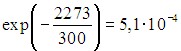. Таким образом, в каждом кубическом сантиметре воздуха при комнатной температуре будет более  колебательно-возбужденных молекул азота и порядка  колебательно-возбужденных молекул кислорода. Вряд ли в этих условиях можно говорить о том, что эти молекулы «жесткие»  и у них только пять степеней свободы, так как колебательной степени свободы у них нет. Тем более, что уже при температуре в 1000 К доли колебательно-возбужденных молекул составят для азота около 3 % и около 10 % для кислорода. В качестве ещё одного примера приведем молекулу , для возбуждения колебаний ядер в которой требуется минимальная энергия всего . Уже при комнатной температуре доля колебательно-возбужденных молекул  составит примерно 20 %. Пренебрегать колебаниями ядер в этой молекуле нельзя уже при комнатной температуре.

Вряд ли разумно говорить, что наличие или отсутствие колебательной степени свободы у двухатомной молекулы зависит от типа молекулы и температуры газа. Это попытка «запихнуть» носящее квантовый характер колебательное движение ядер в рамки неадекватного в данном случае классического (не квантового) описания. Колебательная степень свободы у двухатомной молекулы есть всегда, а вот вклад колебательного движения ядер в такой молекуле во внутреннюю энергию газа, в теплоемкости  и , в показатель адиабаты  и другие характеристики газа может быть пренебрежимо мал, если выполняется неравенство

где  введенная выше постоянная Больцмана. При выполнении противоположного неравенства

пренебрегать колебательным движением ядер никак нельзя. Классическое (не квантовое) описание колебательного движения ядер в молекулах возможно лишь в случае малой энергии возбуждения колебательного движения и достаточно высокой температуры, а именно: при выполнении неравенства

 ,

которое на практике выполняется лишь в редких исключительных случаях вроде молекулы . В том воздухе, которым мы можем относительно комфортно дышать, колебания ядер в молекулах  и   классической механикой не описываются.

Вернемся теперь к идеальному газу. Мы видели, что средняя кинетическая энергия поступательного движения молекул равна

и что поступательному движению соответствуют три степени свободы. Значит, на одну степень свободы, в состоянии термодинамического равновесия приходится средняя энергия

При классическом (не квантовом) описании все виды движения равноправны. Молекулы сталкиваются, и при этом легко может случиться так, что энергия поступательного движения перейдет в энергию вращательного движения. Поэтому на каждую из вращательных степеней свободы должно приходиться в среднем то же количество энергии —

Это утверждение известно как закон Больцмана о равнораспределении энергии по степеням свободы. Похожим образом столкновения молекул могут породить и колебательные движения ядер в них, так что классический закон равнораспределения относится также и к колебательным степеням свободы молекул. Но здесь есть одна тонкость. Если поступательному и вращательному движениям соответствует только кинетическая энергия, то гармонический осциллятор (одна колебательная степень свободы) обладает в среднем строго равными кинетической и потенциальной энергиями. Поэтому, в среднем, в состоянии термодинамического равновесия, в условиях применимости классического описания колебательного движения, на одну колебательную степень свободы приходится энергия в два раза большая

 

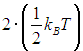
Если ввести эффективное число по той же формуле, что и введенное выше , а именно

с тем принципиальным отличием, что параметр  уже вовсе не есть номинальное число колебательных степеней многоатомной молекулы, то средняя энергия одной молекулы будет равна

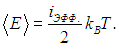
Значит, полная внутренняя энергия U газа будет в N раз больше (N — число молекул газа):

 

Уравнение Клапейрона — Менделеева может быть записано как

или в несколько другой форме

С так называемым показателем адиабаты

мы познакомимся в следующей главе, где прояснится смысл этого термина. Как было показано выше, колебательное движение ядер в молекулах возбуждается лишь по достижении достаточно высоких температур (Т > 1000 К), поэтому их вклад во внутреннюю энергию газа для большинства молекул при обычных (близких к комнатной) температурах ничтожен, мы не будем его учитывать, то есть, если не оговорено противное будем считать, что

,

где   и   равны номинальному числу поступательных (всегда 3) и вращательных (3 или 2) степеней свободы, соответственно структуре молекулы.

Пример. В комнате объемом 75 м³ находится двухатомный газ (воздух) при температуре t = 12 °С (T = 285 К). Включают обогреватель и поднимают температуру воздуха до t₂ = 22 °С (Т₂ = 295 К). Поскольку комната не герметизирована, давление газа остается все время постоянным и равным 100 кПа. Найдем изменение внутренней энергии газа в комнате и определим, какая энергия была потрачена на обогрев окружающей среды.

Ответ несколько неожидан: согласно (1.19) внутренняя энергия газа в комнате не изменилась, поскольку остались прежними и его давление, и объем. С другой стороны, часть газа из комнаты вышла: если вначале там содержалось

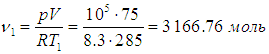
вещества, то после подогрева осталось лишь

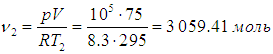
На улицу вышло

 

воздуха или

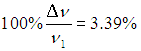
его начального количества.

Подсчитаем, сколько энергии ушло на «обогрев» улицы. Условно разобьем весь процесс на два этапа (на самом деле они происходят одновременно, но это не меняет сути дела). На первом этапе мы обогреваем герметичную комнату. Начальная внутренняя энергия газа определяется формулой

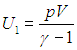
С учетом того, что для двухатомного газа

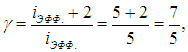
получаем

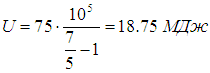
Поскольку внутренняя энергия пропорциональна абсолютной температуре, после нагрева герметичной комнаты оказывается, что

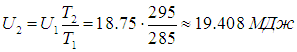
то есть от печки получена энергия

На втором этапе мы удаляем из комнаты 3,39 % подогретого воздуха, и вместе с ним ту же долю энергии. Удаляемая энергия

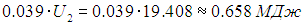
в точности равна энергии, полученной от печки. Иным путем мы снова пришли к тому же выводу.

Итак, теперь окончательно ясно, что ушедший на улицу воздух унес с собой всю энергию, полученную от печки. В чем же тогда роль печки? Стоило ли ее вообще включать, если она обогревает только улицу? Полезный эффект печки состоит в том, что при температуре в 12 градусов теплопотери человека в окружающий воздух столь велики (несмотря на то, что он одет, надо полагать), что система терморегуляции организма справляется с трудом с поддержанием нормальной температуры и сигнализирует об этом: холодно человеку, некомфортно! А при температуре 22 градуса теплопотери существенно меньше, меньше нагрузка на систему терморегуляции — человек чувствует себя вполне комфортно и у него не возникает желания включать обогреватель.

 

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 50–61, ч. I, § 6, — теоретический расчет теплоемкостей, приводятся  экспериментальные зависимости теплоемкости при постоянном объеме в широком интервале температур для десяти конкретных газов.