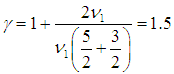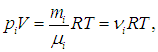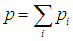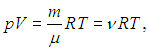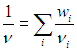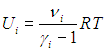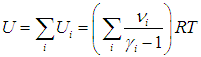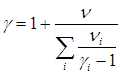1.5. Смеси газов
Возникает естественный вопрос: какими уравнениями описываются смеси идеальных газов? Ведь с чистыми газами нам редко приходится встречаться в природе. Например, наша естественная среда обитания — воздух — состоит из азота N2 (78,08 %), кислорода O2 (20,95 %), инертных газов (0,94 %), углекислого газа СO2 (0,03 %).
Пусть в некотором объеме V при некоторой температуре Т содержится смесь газов (которые мы будем нумеровать
индексом i ). Роль каждого компонента смеси будем характеризовать массовой долей:
|
|
|
(1.20) |
где mi — масса i-го компонента. Наша задача — написать уравнение, подобное уравнению Клапейрона — Менделеева, и разобраться с эффективным числом степеней свободы смеси, где могут содержаться и одноатомные, и многоатомные молекулы.
Прежде всего, заметим, что мы рассматриваем идеальные газы. Молекулы не взаимодействуют друг с другом, и потому каждый компонент не мешает любому другому «жить» в том же общем сосуде. Различные газы в сосуде, в силу их предполагаемой идеальности, просто «не замечают» друг друга. Поэтому для каждого из компонентов справедливо одно и то же уравнение Клапейрона — Менделеева:
|
|
|
(1.21) |
где ni — число молей вещества в i -м компоненте. Полное число n молей в смеси равно сумме числа молей ni в каждом из компонентов:
![]()
Аналогично, полная масса смеси равна сумме масс каждого из компонентов
![]()
и естественно определить молярную массу смеси m как массу одного моля смеси:
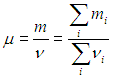
Введем величину, называемую парциальным давлением.
|
Парциальное давление pi — это давление, оказываемое i-м компонентом газовой смеси. |
Имеет место закон Дальтона для газовой смеси:
|
Полное давление газовой смеси равно сумме всех парциальных давлений
|
Суммируя левые и правые части (1.21), приходим к стандартной форме уравнения Клапейрона — Менделеева
|
|
|
(1.23) |
где m, μ, n определяются из условия конкретной задачи. Например, если заданы массовые доли компонентов, то молярную массу смеси находим из соотношения
|
|
|
(1.24) |
Внутренняя энергия Ui i-го компонента смеси определяется в соответствии с формулами (1.16) и (1.19):
|
|
|
(1.25) |
С одной стороны, полная внутренняя энергия смеси равна сумме энергий каждого компонента:
|
|
|
(1.26) |
С другой стороны, запишем стандартное выражение вида (1.25)
|
|
|
(1.27) |
Сравнивая (1.26) и (1.27), получаем формулу для показателя адиабаты смеси
|
|
|
(1.29) |
Найдя массу моля и показатель адиабаты смеси, мы можем пользоваться всеми формулами, полученными ранее для «чистых» идеальных газов.
Пример. Дана смесь кислорода O2 (компонент 1) и аргона Ar (компонент 2), причем количества вещества обоих компонентов одинаковы n1 = n2. Найдем показатель адиабаты смеси.
Показатель адиабаты двухатомного кислорода равен
![]()
а одноатомного аргона
![]()
Поэтому для смеси газов на основании (1.29) получаем