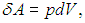2.1. Первое начало термодинамики

Примером функции состояния системы является ее внутренняя энергия U. Она составляется из кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия между молекулами, кинетической энергии атомов внутри молекул, потенциальной энергии взаимодействия между атомами внутри молекул, а также кинетической и потенциальной энергии частиц, входящих в состав атомов (ядер и электронов). Внутренняя энергия не включает кинетическую и потенциальную энергии, которыми система может обладать как целое (скажем, при движении сосуда с газом или помещении газа во внешнее потенциальное поле). Каждый раз, когда система оказывается в том же состоянии (например, при каких-то конкретных температуре и давлении), ее внутренняя энергия принимает присущее этому состоянию значение, независимо от способа, каким система приведена в данное состояние. При переходе из состояния 1 в состояние 2 изменение внутренней энергии равно разности значений внутренней энергии в этих состояниях

и также не зависит от того, какие процессы перевели систему из состояния 1 в 2.

Внутренняя энергия системы может изменяться двумя способами:

• путем совершения над системой работы А;
• путем передачи ей количества теплоты Q.

Совершение работы сопровождается перемещением внешних тел, действующих на систему. Рассмотрим заключенный под поршнем в сосуде газ (рис. 2.1-1).

Рис. 2.1. Расширение газа под поршнем (1) и графическое изображение (2) производимой им работы

При перемещении поршня на расстояние dl газ совершает работу

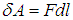
Если S — площадь поперечного сечения сосуда, то силу F можно выразить через давление (F = pS), которое при малом перемещении поршня можно считать постоянным. Перемещение выражается через изменение объема газа

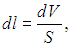
так что элементарная работа, совершенная газом, представляется в виде

то есть численно равна площади заштрихованного участка на (pV) — диаграмме процесса (рис. 2.1-2).

Этот тип передачи энергии всегда связан с перемещением макроскопических частей системы и внешних тел. Если бы такого перемещения не происходило, то есть не менялся бы объем системы (dV = 0), то, как следует из соотношения (2.2), газ не мог бы совершить работы (dА = 0). При увеличении объема системы работа положительна (система совершает работу), а при уменьшении — отрицательна (работа совершается внешними силами над системой).

 

При конечном изменении объема системы совершаемая газом работа является суммой всех элементарных работ dА и записывается в виде интеграла

Графически такая работа изображается площадью криволинейной трапеции под графиком процесса на (р,V) — диаграмме (см. рис. 2.2). Видно, что эта площадь зависит не только от положения концевых точек (р₁,V₁) и (р₂,V₂), но и от всего характера процесса перехода из состояния 1 в состояние 2 (то есть от вида кривой р = р(V).

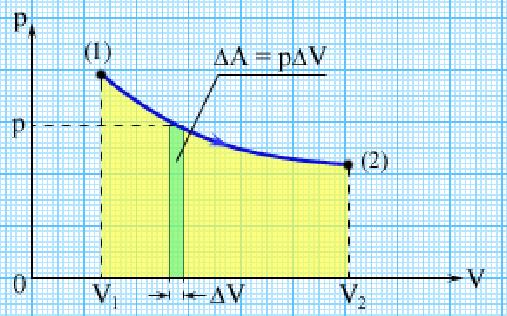
Рис. 2.2. Работа, совершаемая газом

Поэтому работа не является функцией состояния системы.

Рассмотрим теперь процесс передачи теплоты системе.

 

Изучение тепловых явлений показывает, что теплообмен между телами может осуществляться тремя способами:

• теплопроводностью;

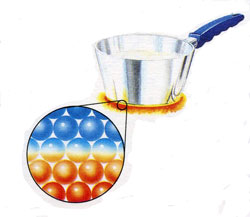
Рис. 2.3. Теплообмен путем теплопроводности

• конвекцией;

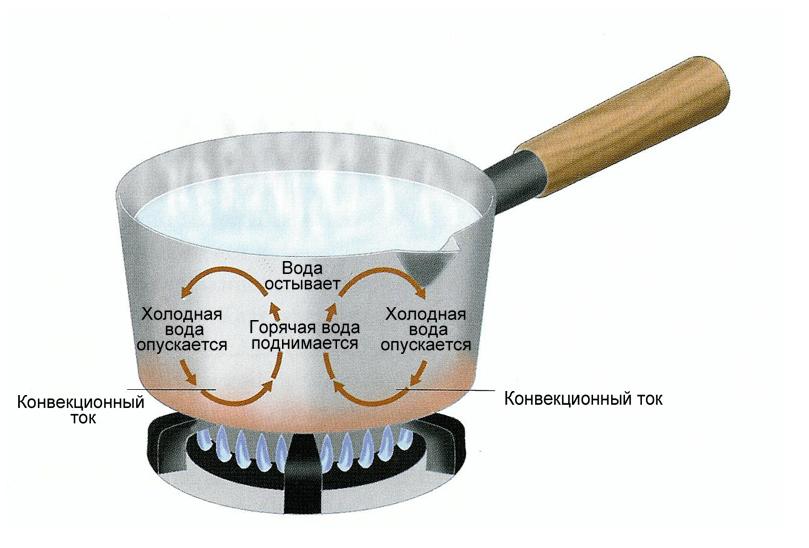
Рис. 2.4. Теплообмен путем конвекции

• излучением.

Рис. 2.5. Теплообмен путем излучения

Тепло, полученное системой, считается положительным, а отданное ею — отрицательным. Поскольку количество теплоты, переданное при теплообмене, связано с изменением энергии движения молекул системы, то о хаотическом беспорядочном движении молекул часто говорят как о тепловом движении.

Будучи одной из форм энергии, теплота измеряется в джоулях (Дж). Но прежде чем была понята связь теплоты и энергии, теплоту измеряли в специальных единицах - калориях. Сообщение одной калории одному грамму воды поднимает ее температуру на один градус Цельсия. Сейчас калория определяется соотношением

Калория все еще применяется в некоторых областях человеческой деятельности. Вспомните, например, калорийность продуктов питания, в которых многие стараются себя ограничить. При окислении 100 г животных жиров освобождается около 1 000 ккал энергии (для других продуктов поменьше: хлеб — 214 ккал, сыр — 313 ккал, сахар — 390 ккал, шоколад — 428 ккал, масло — 734 ккал).

Пример. Человек массой 90 кг, желающий похудеть, ежедневно 10 раз взбегает по лестнице на 12-й этаж (расстояние между этажами порядка 3 м). Определим, какой вес он потеряет за неделю, если его диета не меняется.

Оценим прежде всего совершаемую за семь дней работу:

Переведем эту работу в калории:

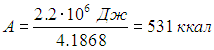
Это соответствует потере приблизительно 50 г массы тела.

 

Дополнительная информация:

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 151–158, часть 2, §§3, 4: описаны эксперименты Джоуля по определению механического эквивалента тепла;

Первое начало термодинамики — это закон сохранения и превращения энергии, примененный к тепловым явлениям (рис. 2.6).

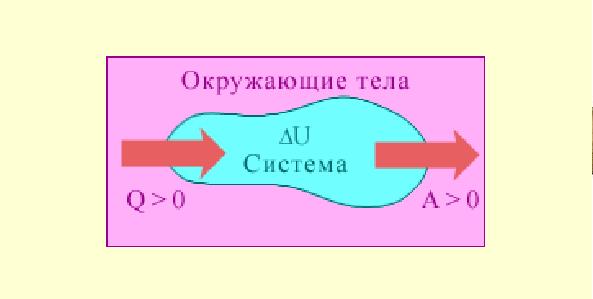
Рис. 2.6. Первое начало термодинамики

При конечных изменениях параметров системы имеем

Как мы видели, внутренняя энергия является функцией состояния системы, а работа зависит от процесса перехода системы из начального состояния в конечное. Отсюда следует, что и теплота не есть функция состояния системы, она тоже зависит от особенностей рассматриваемого процесса. Именно поэтому мы использовали символы dА и dQ для элементарных приращений этих величин: в варианте написания dA, dQ могло бы создаться ложное впечатление, что мы имеем дело с дифференциалами функций А, Q, которых на самом деле не существует.

 

 

Дополнительная информация

http://kvant.mirror1.mccme.ru/pdf/1998/03/kv0398mitugov.pdf — Журнал Квант, 1998 г. № 3, стр.7–9, В.Митюгов, О квантовой природе теплоты.