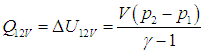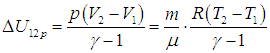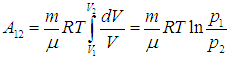2.2. Работа идеального газа в различных процессах

Имея уравнение состояния (1.7) идеального газа, мы найдем совершаемую им работу при некоторых типичных процессах. Заодно определим количество теплоты, получаемое от внешнего источника.

1. Изохорный процесс. При изохорном нагревании или охлаждении (соответственно, прямые 1–2 и 1–3 на рис. 2.7) работа просто равна нулю, поскольку объем не меняется.

Рис. 2.7. определению работы в изохорном процессе

Получаемое количество теплоты (обозначим Q₁₂ при V = const через Q_12V) полностью идет на изменение внутренней энергии газа (см. (1.19))

Ту же самую величину можно выразить через изменение температуры газа

2. Изобарный процесс. Поскольку в этом процессе р = const, то давление можно вынести из-под знака интеграла в (2.3). Тогда получаем (рис. 2.8)

Рис. 2.8. Работа в изобарном процессе

Изменение внутренней энергии газа следует из (1.17) – (1.19)  1.17

1.18

   1.19:

Складывая (2.8) и (2.9), находим количество теплоты, переданное газу в этом процессе:

Пример 1. Пусть система получила при постоянном давлении определенное количество теплоты Q. Найдем, какая часть расходуется на совершение работы А, а какая — на увеличение внутренней энергии газа. Определим также, как зависит ответ от вида используемого газа.

Из формул (2.8) и (2.9) сразу следует, что

Чем больше g, тем большая часть тепла переходит в работу: для одноатомных газов

для двухатомных (без учета колебаний ядер, при двух вращательных степенях свободы)

и для многоатомных газов (без учета колебаний ядер, при трех вращательных степенях свободы)

Заметим, что мы излагаем достаточно общий подход, который применим не только к идеальным газам. Для иных систем может измениться уравнение состояния, как следствие изменятся выражения для совершенной работы, но принципы их вывода остаются одними и теми же. Приведем пример. Пусть для некоторой системы давление, температура и объем связаны соотношением

Найдем выражение для работы такой системы при изменении ее температуры от Т₁ до Т₂ при постоянном давлении. Поскольку давление постоянно, имеем для работы в изобарном процессе стандартное выражение

Используя уравнение состояния (2.11), находим отсюда

 

3. Изотермический процесс расширения (или сжатия) газа может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной разности температур. Для этого теплоемкость внешней среды должна быть достаточно велика, и процесс расширения (или сжатия) должен происходить достаточно медленно. Диаграмма изотермического расширения представлена на рис. 2.9.

Рис. 2.9. Работа при изотермическом расширении системы

Используя уравнение состояния и выражение (2.2) для элементарной работы, находим

Далее используем общее выражение (2.3) для работы при конечном изменении объема

Поскольку объем обратно пропорционален давлению, тот же результат можно представить в виде

Так как внутренняя энергия идеального газа не меняется при изотермическом процессе, в работу преобразовалась вся теплота, полученная от источника:

Пример 2. Расширяясь, водород совершил работу 6 кДж. Найдем количество теплоты, подведенное к газу, если процесс протекал: а) изобарно; б) изотермически.

 

Рассмотрим сначала изобарное расширение. Из формул (2.8) и (2.10) следует связь количества теплоты и совершенной работы:

Мы использовали значение g = 7/5 для двухатомного газа. Для изотермического расширения, как мы видели, полученное количество теплоты просто равно произведенной работе:

Видео 2.1. Работа нагретого газа над вертушкой.

 

Дополнительная информация

http://kvant.mirror1.mccme.ru/ — Журнал Квант, 2004, № 3, стр. 32–33, А. Леонович «А так ли хорошо знакома вам теплопередача?», — попробуйте ответить на оригинальные вопросы, связанные с теплообменом.