2.6. Влажность

Теоретическая изотерма Ван-дер-Ваальса отличается от экспериментальной. Иначе и быть не может, так как область между минимумом и максимумом описывает нестабильное состояние системы, которое не может быть реализовано. В этой области давление растет при увеличении объема и падает при уменьшении. Представим себе какое-нибудь состояние в этой области (точку на растущей ветви графика). Если в результате флуктуации внешняя сила, удерживающая газ в некотором объеме, несколько возрастет, то объем газа слегка уменьшится, и это, в отличие от обычных состояний, приведет к уменьшению давления газа. Испытывая меньшее сопротивление, внешняя сила сильнее сожмет газ, давление его еще уменьшится и т. д. Словом, такое состояние столь же нестабильно, как и равновесие иглы, стоящей на кончике.

Поэтому если газ изотермически сжимать (при Т < Т_с), то при некотором значении объема V давление газа перестает меняться. На рисунке 2.16 это соответствует точке 1 на горизонтальном участке изотермы.

Рис. 2.16. Изотермы Ван-дер-Ваальса: штриховая часть изотермы при Т = 0,9Т_С соответствует неустойчивым состояниям газа (1); область насыщенного пара (2) получена соединением концов горизонтальных участков изотерм при различных температурах

На этом участке, происходит конденсация газа в жидкость: над жидкостью образуется насыщенный пар, давление которого р_Н(T) зависит только от температуры и потому не меняется (рис. 2.17).

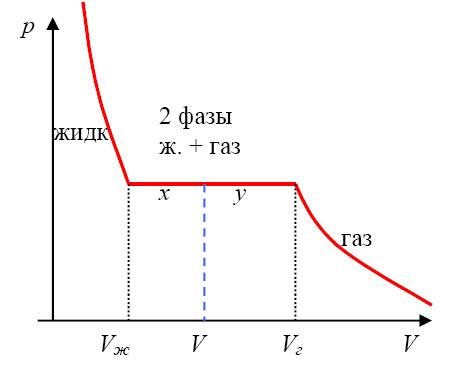
Рис. 2.17. Экспериментальная изотерма реального газа

Покажем, что давление термодинамически равновесной двухфазной системы зависит только от её температуры, для этого рассмотрим условия термодинамического равновесия в такой системе.

В отсутствие обмена частицами, необходимыми условиями термодинамического равновесия двух тел являются равенства температур и давлений. Равенство температур необходимо для того, чтобы отсутствовал теплообмен между телами. Равенство давлений — для того, чтобы ни одно из этих тел не совершало работу над другим телом. При рассмотрении равновесия двух фаз одного и того же вещества, например, жидкости (жидкая фаза) и ее пара (газовая фаза), необходимо дополнительно учитывать возможность обмена частицами. При испарении молекулы покидают жидкую фазу, переходя в газовую, при конденсации — наоборот: молекулы из газа переходят в жидкость. В состоянии термодинамического равновесия средние скорости этих процессов должны быть равны, тогда обмена частицами — в среднем — не будет. Пусть за время  dt  из жидкости в пар перешло dN_ж-п молекул, а из пара в жидкость — dN_п-ж молекул. Дополнительным необходимым условием равновесия жидкой и газовой фаз является равенство скоростей испарения  и конденсации .

Таким образом, должно выполняться три условия равновесия двух фаз:

 

где Т_п, Р_п, Т_ж, Р_ж — температура и давление пара и жидкости; Т и Р — их равновесные значения.

Как отмечено в (2.49), скорости испарения и конденсации в силу ряда причин зависят и от давления, и от температуры соответствующих фаз (N_исп — жидкой, N_конд — газовой). Укажем лишь на некоторые, наиболее очевидные. Чтобы покинуть жидкость, молекула должна преодолеть межмолекулярное притяжение и, следовательно, обладать достаточной для этого кинетической энергией. Чем выше температура жидкости, тем больше таких молекул, и, следовательно, скорость испарения. Для перехода из газа в жидкость молекула должна по крайней мере подлететь к поверхности жидкости. Следовательно, скорость конденсации пропорциональна потоку молекул, т. е. µ n < v >, здесь n — концентрация молекул, а < v > — их средняя скорость Чем выше давление газа, тем (при Т = const) выше n и, соответственно, N_конд; чем выше температура газа, тем больше <v> µ T^1/2 и (при n = const) N_конд.

Заменив в (2.49) давления и температуры фаз на их равновесные значения Р и Т из (2.47) и (2.48), получаем уравнение: 

                                         

связывающее давление насыщенного пара Р с температурой системы Т:

Таким образом, давление насыщенного пара зависит только от температуры системы «жидкость — пар». Соответствующая зависимости (2.51) кривая на плоскости (Р, Т) называется кривой испарения.

Совершенно аналогично можно показать, что давление в двухфазной системе кристалл – жидкость или в системе кристалл — газ также зависит только от температуры этой системы. Отличие состоит только в том, что вместо условия равенства скоростей испарения и конденсации (2.49) необходимо рассмотреть условие равенства скоростей плавления и кристаллизации в первом случае и скоростей сублимации и обратного процесса перехода из газовой фазы в кристаллическую ˗ во втором случае.

Вернемся к рассмотрению системы жидкость – пар.

При дальнейшем уменьшении объема газа (сжатии) все большая его часть переходит в жидкое состояние. Наконец, при значении объема, соответствующем точке 2, весь газ переходит в жидкость, горизонтальный участок изотермы заканчивается и давление резко возрастает. Если построить такие горизонтальные участки изотерм для разных температур Т < Т_с , то они заполнят область, граница которой показана штрихпунктирной линией на рисунке 1-2. Эта область (насыщенный пар) соответствует сосуществованию жидкой и газообразной фаз, справа от нее лежит область газообразной фазы, слева — жидкой.

При критической температуре Т = Т_с горизонтальный участок изотермы стягивается в точку (показана звездочкой на рис. 1), называемую критической точкой.

Рассматривая рисунки, можно прийти к следующим выводам:

• При температуре выше критической вещество может существовать только в газообразном состоянии. Никаким сжатием газ при Т > Т_с нельзя превратить в жидкость. В критической точке, определяемой параметрами состояния р_с , V_c и Т_с , исчезает различие между газом и жидкостью.
• Давление насыщенного пара р_Н(Т) не может превышать критического давления р_с.
• Объем вещества в жидком состоянии не может превышать его критический объем.

Видео 2.2. Критическое состояние эфира.

 

Пример 1. Найдем наибольший объем V, который может занимать вода массой 1 кг.

Как было сказано, из вида изотерм Ван-дер-Ваальса на рис. 2.9 следует, что наибольший объем данная масса жидкости может занимать в критической точке. Поэтому используем (2.44):

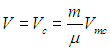
Значение V_mc берем из таблицы 2, откуда следует

— в три раза больше объема воды в обычных условиях!

Заметим, что зависимость давления насыщенного пара от температуры р_Н(Т) проявляется, в частности, в изменении температуры кипения воды при подъеме в горы. Точка кипения определяется из равенства давления насыщенного пара атмосферному давлению. Понижение последнего приводит к более низкой изотерме на нашем рисунке, то есть. к понижению температуры кипения.

Напомним заодно, что вместе с атмосферным давлением и температурой воздуха в сводках погоды сообщают и его относительную влажность. Под ней понимается выраженное в процентах отношение парциального давления водяного пара, содержащегося в воздухе, к давлению насыщенного пара при данной температуре. Таким образом, 100 % влажность вовсе не означает, что вместо воздуха мы стали дышать водой. Давление насыщенного водяного пара при некоторых значениях температуры приведено в табл.

Давление насыщенных паров воды

Пример 2. По радио передали, что атмосферное давление равно р = 757 мм ртутного столба (плотность ртути ρ = 3,55 г/м³), относительная влажность воздуха r = 86 %, а температура воздуха 20 °С. Найдем абсолютную влажность воздуха r_а (то есть массу водяных паров в единице объема), а также определим, какую долю h от атмосферного давления составляет парциальное давление водяных паров.

Сначала определим значение атмосферного давления в единицах СИ. Давление ртутного столба высотой h равно

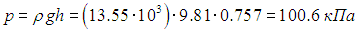
По табл. 3 находим давление насыщенных паров при данной температуре воздуха: р_Н = 2,34 кПа. Парциальное давление паров воды

и мы можем уже ответить на второй вопрос задачи:

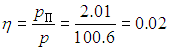
Поскольку искомая абсолютная влажность есть не что иное, как плотность водяного пара

применяя уравнение Клапейрона — Менделеева для водяного пара, немедленно находим

 

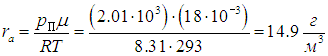
Пример 3. Если температура в предыдущем примере понизится, то в воздухе может появиться туман. Определим, при какой температуре это произойдет. Найдем также, какое количество росы выпадет на землю при понижении температуры до 10 °С.

Видео 2.3. «Генератор» тумана: теплая вода и жидкий азот.

Надо найти температуру t_p (ее называют точкой росы), при которой давление р_Н насыщенного водяного пара станет равным полученному выше парциальному давлению паров воды р_П = 2,01 кПа. Тогда относительная влажность воздуха достигнет 100 %, и дальнейшее понижение температуры приведет к конденсации «излишков» пара. В табл. нет значения 2,01 кПа для давления насыщенного пара, но можно утверждать, что искомая температура находится в интервале от 15 °С до 20 °С. Поскольку он не столь велик, для более точного определения точки росы используем линейное приближение: будем считать, что в указанном интервале зависимость давления от температуры является линейной:

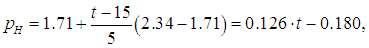
где давление измеряется в кПа, а температура — в градусах Цельсия. Приравнивая р_Н и р_П, находим точку росы

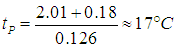
При понижении температуры до значения t₁=10 °С давление насыщенного пара понижается до р_H1 = 1,23 кПа, как следует из той же таблицы, то есть становится меньше прежнего р_Н = 2,01 кПа. В этой же пропорции уменьшается плотность водяных паров:

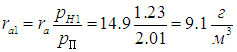
Следовательно, из каждого кубометра воздуха на землю выпадет

 

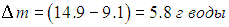
Дополнительная информация

http://kvant.mirror1.mccme.ru/ — Журнал Квант, 2004, № 2, стр. 23–25, В. Можаев «Насыщенные и ненасыщенные водяные пары» — решается несколько интересных задач, касающихся испарения воды;

http://www.alleng.ru/d/phys/phys62.htm — Тульчинский М.Е.  Качественные задачи по физике, Изд. Просвещение, 1972 г.; задача № 611 на насыщенные пары;

http://kvant.mirror1.mccme.ru/1996/05/otkuda_berutsya_oblaka.htm — Журнал Квант, 1996 г. № 5, стр.40–41, А. Айзенкрафт, Л. Кирпатрик, Откуда берутся облака?

http://experiment.edu.ru/catalog.asp?cat_ob_no=12329&ob_no=12384 — Демонстрация кипения жидкости при пониженном давлении;

http://experiment.edu.ru/catalog.asp?cat_ob_no=12329&ob_no=12390 — Демонстрация опыта по расширению воды при замерзании;

http://by-chgu.ru/category/physics — Физическая энциклопедия, т. 1, М., 1988, стр.278–279 — описано использование пересыщенного пара для регистрации электрически заряженных частиц в камере Вильсона;

http://by-chgu.ru/category/physics — Физическая энциклопедия, т. 4, М., 1994, стр. 177–179 — описано использование перегретой жидкости для регистрации электрически заряженных частиц.

 

Видео 2.4. Перегретая жидкость: добавление центров парообразования приводит к вскипанию перегретой жидкости.

Наличие «внутреннего» давления

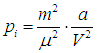
газа Ван-дер-Ваальса приводит к тому, что внутренняя энергия такого газа по сравнению с внутренней энергией идеального газа U_ид включает добавку — потенциальную энергию взаимодействия молекул между собой. Эта дополнительная потенциальная энергия получается равной

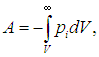
где знак «минус» означает притяжение между молекулами. Тогда для внутренней энергии газа Ван-дер-Ваальса имеем соотношение

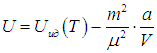
Данная формула отражает тот факт, что при увеличении объема газа производится работа против сил притяжения между молекулами. Из нее следует теоретическое объяснение эффекта Джоуля — Томсона (рис. 2.18).

Рис. 2.18. Эффект Джоуля — Томсона

В этом эффекте газ адиабатно расширяется в пустоту. Поскольку нет подвода тепла и газ не совершает работы против внешнего давления, его внутренняя энергия U должна оставаться постоянной. Для идеального газа это эквивалентно постоянству температуры. Но для газа Ван-дер-Ваальса уменьшение вычитаемого в выражении для внутренней энергии при U = const влечет за собой уменьшение первого члена, то есть понижение температуры. Этим эффектом пользуются при сжижении газов. В веществах, где доминирует отталкивание между молекулами, добавка к U положительна, и наблюдается повышение температуры при адиабатном расширении, то есть обратный эффект Джоуля — Томсона.

 

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 151–158, часть 2, §§ 3, 4: описаны эксперименты Томсона (Кельвина) по дросселированию газов через пористую перегородку;

http://kvant.mirror1.mccme.ru/1995/01/rasshirenie_gaza_v_pustotu.htm — Журнал Квант, 1995 г. № 1, стр. 37,  А. Стасенко, Расширение газа в пустоту.