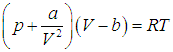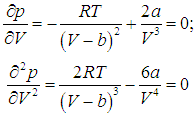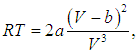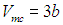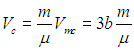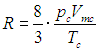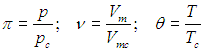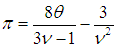2.5. Уравнение Ван-дер-Ваальса

Уравнение Клапейрона — Менделеева следует из молекулярно-кинетической теории в предположении идеальности газа. Если мы хотим описывать поведение реальных систем, надо учесть взаимодействие молекул между собой. Точный учет межмолекулярных сил — задача чрезвычайно трудная. Поэтому было предложено несколько модификаций уравнения состояния идеального газа, которые могли бы учесть основные особенности реальных систем. Наиболее удачной попыткой стало уравнение Ван-дер-Ваальса, при получении которого вносились поправки в уравнение состояния идеального газа

В подходе Ван-дер-Ваальса, во-первых, принимается во внимание, что молекулы имеют конечные размеры. Если обозначить собственный объем всех молекул в моле вещества буквой b, то для движения молекул остается свободный объем

и именно он должен фигурировать в уравнении состояния. Во-вторых, учитывается, что молекула, подлетающая к стенке сосуда, «чувствует» притяжение других молекул, которое уравновешивалось, когда молекула была внутри сосуда. Дополнительная сила, направленная внутрь сосуда, эквивалентна дополнительному давлению p_i, (его называют «внутренним» давлением газа). Поэтому вместо давления р газа на стенки сосуда уравнение состояния должно содержать сумму р+р_i.

Как зависит внутреннее давление p_i от параметров системы? Сила, действующая на каждую молекулу, пропорциональна концентрации п молекул в системе. Число подлетающих к стенке молекул также пропорционально п, и потому внутреннее давление пропорционально квадрату концентрации частиц:

Обозначая коэффициент пропорциональности буквой а, приходим к уравнению Ван-дер-Ваальса

(2.35)

Для одного моля вещества это уравнение упрощается:

(2.36)

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 38–47, ч. I, § 6, п.п. б, в. — обсуждается уравнение Ван-дер-Ваальса и приводятся экспериментально полученные межмолекулярные потенциальные энергии взаимодействия для гелия, водорода, аргона и углекислого газа;

http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 246–248 — детальная информация о силах межмолекулярного притяжения в газе Ван-дер-Ваальса.

Рассмотрим вид изотерм газа Ван-дер-Ваальса на (р,V) - диаграмме (рис. 2.14). Они описываются функцией

(2.37)

При достаточно высоких температурах и больших объемах введенными поправками можно пренебречь, и вид изотерм получится обычным. При понижении температуры вид изотерм все более искажается и при некотором критическом значении температуры Т_с данная изотерма приобретает точку перегиба (критическую точку) с координатами (р_с, V_c), в которой равны нулю первая и вторая производные давления по объему. При дальнейшем понижении температуры точка перегиба превращается в минимум и максимум функции p(V).

Рис. 2.14. Изотермы газа Ван-дер-Ваальса

Найдем сначала значения параметров, соответствующих критической точке. Берем первую и вторую производные функции (2.37) и приравниваем их нулю:

(2.38)

Решение этой пары уравнений даст нам критические значения T_c и V_c. Находя из первого уравнения значение

(2.39)

подставляем его во второе уравнение, откуда тогда следует

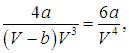
или

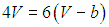
Получаем сначала значение молярного критического объема

(2.40)

Подставляя его в уравнение (2.39), находим критическую температуру

(2.41)

Наконец, подставляя найденные значения Т_с, V_c в уравнение (2.37), находим критическое давление

(2.42)

Эти критические значения получены для одного моля вещества. Чтобы найти их для произвольного числа молей, заметим, что при переходе от уравнения (2.36) к (2.35) надо произвести масштабное преобразование

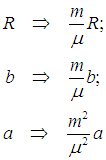
Выполняя то же преобразование в формулах для критических значений термодинамических параметров, убеждаемся, что критические температура и давление не изменяются, а объем преобразуется естественным образом:

(2.43)

Значения критических параметров берутся из данных эксперимента. Отметим, что газовая постоянная R также может быть выражена через критические параметры:

(2.44)

Для каждого реального газа следует вычислять свою индивидуальную газовую постоянную R, которая будет отличаться от универсальной газовой постоянной N_Ak_B идеального газа. Этому не следует удивляться, учитывая феноменологический приближенный характер уравнения Ван-дер-Ваальса. Значения критических параметров некоторых веществ и их газовая постоянная приведены в табл. 2.

Таблица 2.

Критические параметры некоторых газов

*Газ*	*Т_с , К*	*р_с , МПа*	*V_m* *, см³/моль*
Не	5.2	0.23	57.5	0.82
Н₂	33.2	1.30	65.5	0.82
0₂	154.8	5.08	78	0.82
С0₂	304.1	7.39	94	0.73
Н₂0	647.3	22.1	56.3	0.62

Возьмем для примера пары воды. Из таблицы следует значение коэффициента

Поделив на число Авогадро, получаем объем одной молекулы

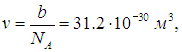
откуда для диаметра молекулы следует оценка

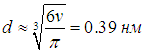
Это действительно близко к размерам молекулы воды, что свидетельствует о правильности модели Ван-дер-Ваальса.

Введем обозначения в виде соответствующих греческих букв для термодинамических параметров, измеренных в единицах их критических значений, то есть для безразмерных отношений:

(2.45)

В этих обозначениях все критические значения термодинамических параметров равны единице, а уравнение Ван-дер-Ваальса (2.36) принимает простой вид

(2.46)

Отметим универсальность этого уравнения, которое может быть использовано даже без точного знания значений критических параметров (но они нужны, конечно, при возвращении к обычным единицам измерения температуры, давления и объема).

На рис. 2.15 представлены изотермы газа Ван-дер-Ваальса для нескольких значений температуры (q=2; 1.1; 1; 0.9; 0.85).

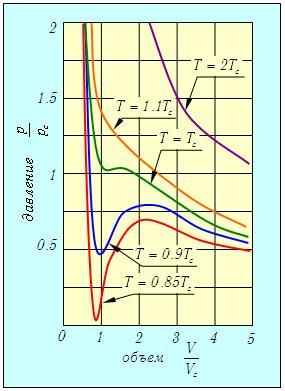
Рис. 2.15. Изотермы газа Ван-дер-Ваальса для различных значений температуры (построены для безразмерных отношений термодинамических параметров р, V , Т к их критическим значениям р_с , V_c , T_c)

При достаточно высоких температурах Т = 2Т_с (q = 2) изотермы Ван-дер-Ваальса совпадают с изотермами идеального газа за исключением области малых объемов. При понижении температуры гиперболы начинают искажаться и при Т = Т_с (q = 1) график имеет точку перегиба при р = р_с , V = V_c (p = 1, u = 1). При еще более низких температурах на изотерме появляются минимум и максимум.

Дополнительная информация

http://www.femto.com.ua/articles/part_1/0356.html — Физическая энциклопедия. «Точка Бойля» на изотермах Ван-дер-Ваальса в координатах (P – PV) разграничивает силы межмолекулярного притяжения и отталкивания.

6/7