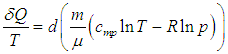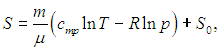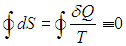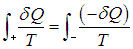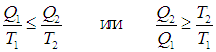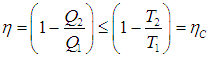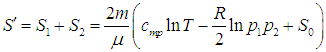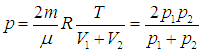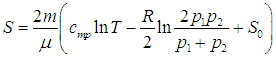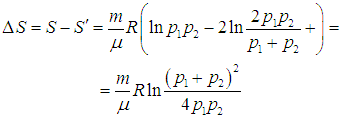5.4. Энтропия

В классической механике и электродинамике мы привыкли к тому, что невозможность какого-то процесса, как правило, связана с каким-то законом сохранения (энергии, импульса, электрического заряда и т. п.). Почему же невозможен вечный двигатель второго рода? Казалось бы, он не нарушает никаких законов сохранения? Чтобы понять это, надо обратиться еще к одной функции состояния системы — к энтропии.

Путь к этой новой для нас функции состояния недолог: надо взять уравнение первого начала термодинамики

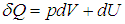
и разделить его обе части на температуру. Прежде всего учтем, что

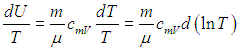
Далее в формуле для элементарной работы

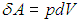
выразим объем через давление и температуру из уравнения состояния (1.7) идеального газа:

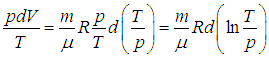
Получим в итоге с использованием соотношения Майера между молярными теплоемкостями

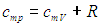
следующее выражение

Правая часть (5.34) представляет собой дифференциал некоторой функции S состояния системы:

где S₀ — постоянная интегрирования, не зависящая от термодинамических параметров системы (давления, объема, температуры). Эта функция S называется энтропией. Получилось так, что величина dQ, не являющаяся дифференциалом какой-либо функции состояния, при делении на T стала таковым:

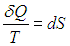
При замкнутом обратимом цикле изменение любой функции состояния (в частности, энтропии) равно нулю:

Кружок на знаке интеграла означает, что интегрирование ведется по замкнутому контуру.

Проверим выполнение (5.19) на примере цикла Карно. Поскольку в этом цикле тепло получается системой и отдается только на изотермах (Т_1,2 = const), температуру можно вынести из-под знака интеграла, и тогда интегрирование даст просто количество теплоты, поделенное на температуру, при которой оно получается или отдается. И действительно, выше было найдено, что на изотермических ветвях цикла при температуре Т₁ газ получает теплоту

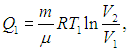
 а при температуре Т₂ — отдает теплоту

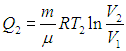
Выполнение равенства

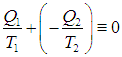
теперь очевидно. Напомним, что получаемое тепло имеет положительный знак, а отдаваемое — отрицательный; мы же определили ранее Q₂ как абсолютную величину отдаваемого тепла, поэтому в формуле появился знак «–».

Проделаем теперь похожие выкладки с произвольным обратимым циклом. Выделим в нем две части: знаком «+» обозначим те фазы процесса, когда система получает тепло, а знаком «–» фазы, когда система отдает тепло. Поскольку полный интеграл равен нулю, аналогичные интегралы по двум частям цикла равны между собой:

Если обозначить через Т₁ максимальную температуру в первой части цикла, то неравенство Т < Т₁ влечет за собой неравенство

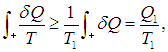
где Q₁ как и прежде означает полное количество теплоты, полученное системой. Если ввести минимальную температуру Т₂ во второй части цикла, то из Т > Т₂ следует

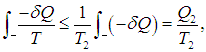
где Q₂ — количество теплоты, отданное системой. Из этих неравенств и соотношения (5.20) следует, что

Наконец получаем неравенство для КПД цикла

С помощью понятия энтропии мы получили иным путем тот же результат: КПД любого цикла не превышает КПД цикла Карно с температурой нагревателя равной максимальной температуре рабочего тела и с температурой холодильника равной минимальной температуре рабочего тела рассматриваемого  цикла. В дальнейшем мы будем опускать указание на то, что сравниваются КПД тепловых машин, работающих в одном и том же интервале температур.

Таким образом, мы убедились, что новая функция состояния — энтропия — связана со вторым началом термодинамики. До сих пор мы ограничивались равновесными (обратимыми) процессами. Рассмотрим пример неравновесного процесса. Пусть в начальном состоянии имеются два одинаковых идеальных газа с равными массами m при одинаковой температуре Т, но разных давлениях р₁ и р₂. Определим изменение энтропии при соединении сосудов с газом.

В первый момент после соединения сосудов, когда газы еще не смешались, энтропия системы равна сумме энтропии газов в отдельных сосудах:

Найдем теперь объемы сосудов:

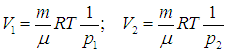
После соединения сосудов масса газа становится равной 2m, а объем — V = V₁ + V₂. Значит, давление р после соединения сосудов равно

Поэтому энтропия газа после соединения сосудов равна

Приращение энтропии  находится из (5.23) и (5.25):

Под знаком логарифма стоит величина, всегда большая единицы. Стало быть, энтропия увеличилась: > 0.

 

Цель этого примера, прежде всего, состоит в том, чтобы на частном случае продемонстрировать, как работает закон возрастания энтропии:

После того как мы соединили сосуды и, тем самым, открыли возможность перемешивания газов, мы получили неравновесное состояние с энтропией, равной сумме энтропий, газы стали перемешиваться, давления выравниваться, система перешла в равновесное состояние с большей, чем ранее энтропией. В результате перехода (благодаря внутренним процессам в системе) из первоначально неравновесного состояния в конечное равновесное состояние энтропия системы возрастает.

 

Дополнительная информация

http://www.femto.com.ua/articles/part_2/4761.html —  Физическая энциклопедия. Энтропия.