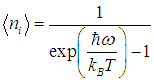7.4. Фононы

Как и внутри молекул, атомы в кристалле совершают малые колебания около фиксированных положений равновесия. Колебания атомов распространяются по кристаллу в виде слабо взаимодействующих волн с волновыми векторами k и частотами 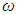(k). Физически нормальные колебания в кристаллах порождают волны деформации кристаллической решетки (то есть упругие волны). Таким образом, движение атомов в кристалле может быть описано как суперпозиция плоских волн различной частоты

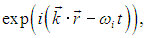
каждой из которых соответствует гармонический осциллятор с частотой 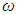(k).

 

Следуя идеям де Бройля, такой упругой волне в кристалле можно сопоставить  квазичастицу с  энергией

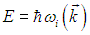
и импульсом

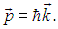
Она носит название фонона.

 

Наше сопоставление можно схематически изобразить следующим образом (рис. 7.4):

Рис. 7.4. Схема «волна — частица»

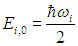
Индекс i стоит для обозначения типа соответствующей волны (продольная, поперечная, характеризующаяся определенным законом дисперсии

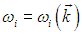
и т. п.), или, как говорят, фононной моды. При квантово-механическом рассмотрении гармонический осциллятор данной фононной моды, как мы уже знаем, может иметь энергию

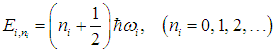
При n_i = 0 мы имеем нулевые колебания с энергией

 

— фонона данной моды в твердом теле нет. При n_i = 1 мы имеем новое состояние с энергией возбуждения

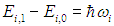
— это и есть квазичастица фонон. При произвольном квантовом числе n_i энергия возбуждения равна

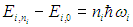
В таком случае мы говорим, что в твердом теле распространяются п_i фононов данной моды i.

 

Используя полученные выше результаты, в случае термодинамического (теплового) равновесия можно найти среднее число фононов <n_i> с частотой w_i. Действительно, мы уже нашли среднюю энергию <e> квантового осциллятора (см. (7.6), где частоту w надо заменить теперь на частоту упругой волны w_i). С другой стороны, эту же энергию можно представить в виде (7.6)

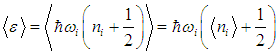
Приравнивая эти выражения, получаем

При низких температурах

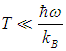
среднее число фононов экспоненциально убывает при T, стремящемся к 0: в системе не возникает возбуждений. Наоборот, при высоких температурах

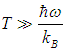
экспоненту в знаменателе можно разложить в ряд Тейлора и получить результат

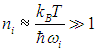
Следовательно, из полученного соотношения вытекает, что при достаточно высокой температуре в кристалле может одновременно возбуждаться неограниченное количество одинаковых фононов, то есть принцип Паули на фононы не распространяется. Напомним, что кванты электромагнитного поля — фотоны, находящиеся в состоянии равновесия со стенками полости, также подчиняются этому распределению.

Представление о фононах широко используется в физике твердого тела. Фононы называют квазичастицами, поскольку они хотя и вполне реальны, но существуют только в кристаллах: вне среды их нет. Идея существования квазичастиц была впервые выдвинута Л.Д. Ландау в 40-х годах прошлого века.

Рис. 7.5. Лев Давидович Ландау

Кроме фононов есть и другие типы квазичастиц. Тепловые колебания решетки можно рассматривать как фононный газ, при низких температурах — идеальный. При очень высоких температурах решетка плавится и модель невзаимодействующих фононов неприменима: они перестают быть свободными. Преимущество представления о фононах состоит в том, что в его рамках свойства твердого тела рассматриваются как свойства ансамбля большого числа независимых квазичастиц — идеального фононного газа. Все представления этой модели могут быть использованы для описания поведения кристаллической решетки.

Можно рассматривать также взаимодействие обычных частиц (электронов, фотонов) с фононами. Так, электроны, обмениваясь фононами, испытывают притяжение. Несмотря на кулоновское отталкивание, может даже образоваться связанное состояние пары электронов. Подобный механизм ведет к явлению сверхпроводимости (будет рассмотрено далее).

Мы уже убедились, что число фононов в твердом теле не постоянно. Фононов тем больше, чем интенсивнее тепловое движение атомов, то есть чем выше температура. C приближением к абсолютному нулю, их число стремится к нулю.