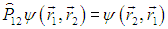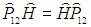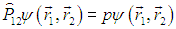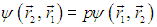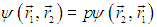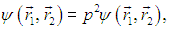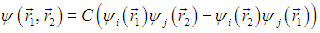7.5. Неразличимость тождественных частиц

Две частицы тождественны, если все их физические свойства в точности совпадают, что исключает возможность экспериментально различать их. В классической теории всегда предполагается, что мы можем в принципе проследить за движением частиц и сказать, какая из них куда полетела. Поэтому в классической теории даже тождественные частицы в принципе различимы. В квантовой механике это не так: принцип неопределенности не позволяет прослеживать траектории и, стало быть, неразличимость частиц имеет принципиальный характер и влияет на результат вычислений.

Пусть, например, система из двух частиц описывается гамильтонианом (оператором энергии)

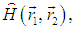
и пусть система находится в состоянии с волновой функцией

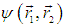
Введем оператор

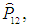
переставляющий частицы местами, то есть обменивающий их радиусы-векторы:

Математически тождественность частиц выражается в инвариантности (неизменности) гамильтониана относительно операции перестановки

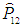
этих частиц, что в квантовой механике записывается как условие коммутации операторов

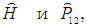
то есть

Это условие обеспечивает физическую неразличимость частиц, поскольку тогда волновая функция  будет также решением уравнения Шредингера с тем же значением  энергии. Действительно, если

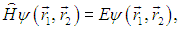
и мы подействуем на обе части этого уравнения оператором коммутации

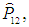
то получим

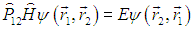
Из-за условия коммутации мы можем пронести оператор коммутации через гамильтониан:

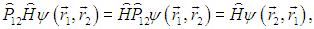
и наше уравнение примет вид

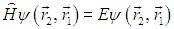
Но мы помним, что коммутирование операторов с гамильтонианом означает сохранение их собственных значений. Найдем собственные значения р оператора коммутации. Для этого надо решить уравнение

С учетом определения (7.31) оператора коммутации, записываем это уравнение в виде

Снова подействуем на обе части (7.34) оператором перестановки частиц:

Из (7.34) и (7.35) получаем, что

то есть р = +1. Таким образом, оператор коммутации может иметь только два собственных значения. При р = 1 волновая функция симметрична относительно операции перестановки частиц:

При р = –1 имеем антисимметричную волновую функцию:

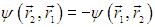
Таким образом, мы получили важный результат:

Справедливо обобщение этого результата:

Какое состояние реализуется — зависит от природы рассматриваемых частиц.

Ранее этими именами мы называли частицы с целым и полуцелым спинами, соответственно. В релятивистском уравнении Дирака, в отличиe от уравнения Шредингера, спин частиц возникает автоматически. Существует фундаментальная теорема Паули:

Эта теорема о связи спина со статистикой является следствием объединения квантовой механики с теорией относительности.

Обратимся для примера к состоянию двух атомных электронов. В пренебрежении взаимодействием между ними волновая функция распадается на произведение волновых функций каждого электрона по отдельности:

Индексы i, j обозначают здесь полный набор квантовых чисел (n, l, т, s), которыми одно состояние отличается от другого. Меняя электроны местами, приходим к состоянию с той же энергией, описываемому волновой функцией

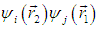
Поэтому в силу принципа суперпозиции возможны состояния, описываемые любой линейной комбинацией этих двух функций, причем все они будут иметь ту же энергию. Однако мы теперь знаем, что для электронов со спином s = 1/2 физический смысл имеет лишь антисимметричная комбинация

Если состояния электронов одинаковы (i = j, то есть совпадают все квантовые числа), то

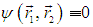
Мы снова пришли к принципу Паули: