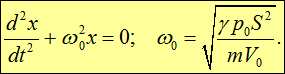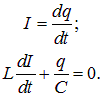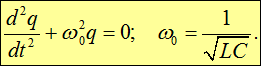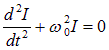1.1. Уравнение гармонических колебаний

В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.

Пружинный маятник

Рис. 1.2. К выводу уравнения движения для пружинного маятника

В положении равновесия (рис. 1.2) сила тяжести  уравновешивается упругой силой  :

 

откуда

где   – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.

Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным  . По закону Гука проекция результирующей силы на ось ОХ  будет тогда равна

Учитывая, что

 

получим

Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.

Запишем теперь уравнение второго закона Ньютона:

Его можно также представить в виде:

Видео 1.1 Грузы на пружинах. Зависимость частоты колебаний от массы груза и жесткости пружины

Математический маятник 

Будем характеризовать отклонение маятника от положения равновесия углом , который образует нить с вертикалью (рис. 1.3).

 

Рис. 1.3. К выводу уравнения движения математического маятника 

При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести  и сила натяжения нити . Соответственно, уравнение движения этой материальной точки имеет вид

.

Проецируя его на направления нормали и касательной к траектории (окружности радиуса ), получаем

Модуль скорости  равен , учитывая, что при движении точки к положению равновесия угол  убывает, а скорость точки  растет, напишем

.

Тогда второе из написанных выше уравнений движения приобретает вид

При малых отклонениях маятника от вертикали, когда ,

получаем:

Видео 1.2 Математический маятник: начальные условия и начальная фаза

Видео 1.3 Математический маятник: запись колебаний песком

Видео 1.4 Математический маятник: синусоида на осциллографе

 

Дополнительная информация

http://physbook.ru/index.php/Kvant._Маятник_с_грузиками – Задача с решением: маятник с несколькими грузиками.

Физический маятник 

Пример физического маятника приведен на рис. 1.4.

Рис. 1.4. К выводу уравнения движения физического маятника

При отклонении маятника от положения равновесия на угол  возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс Cмаятника.

Рассматривая  как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков  и  можно объяснить тем, что векторы  и  направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:

Ограничимся рассмотрением малых отклонений от положения равновесия:

В этом случае уравнение колебаний принимает вид:

 В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен

и мы приходим к уравнению (1.6) движения математического маятника.

Видео 1.5 Физический маятник. Центр качания

Колебания поршня в сосуде с идеальным газом

Рассмотрим цилиндр с площадью поперечного сечения , в который вставлен поршень массы  (рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты , над поршнем воздух с постоянным (атмосферным) давлением . Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен  и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом

В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления  и давления , оказываемого поршнем. Обозначим это результирующее давление :

 Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона

откуда

Здесь  — показатель адиабаты, зависящий от числа степеней свободы молекул газа.

При малых колебаниях, когда изменение объема газа  много меньше его «равновесной» величины , то есть когда

выражение (1.11)  можно разложить в ряд Тейлора:

На поршень действуют три силы: сила атмосферного давления , сила давления газа под поршнем  и сила тяжести . Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей  этих сил:

Используя (1.13), уравнение движения поршня

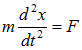
можно записать в следующем виде

 

Видео 1.6 Колебания воды в U-образной трубке

Видео 1.7 Крутильные колебания. Зависимость частоты от момента инерции и жесткости подвеса

Рассмотрим колебательный контур, состоящий из конденсатора емкостью C и катушки индуктивностью L (рис. 1.6).

 

Рис. 1.6. Электромагнитный колебательный контур: 1 – t = 0; 2 – t = Т/4; 3 – t = Т/2; 4 – t = 3Т/4; 5 – t = Т

Сопротивлением катушки и проводов пренебрегаем. Пусть в цепи идет ток I, заряжающий конденсатор:

Так как внешняя ЭДС к контуру не приложена, то ЭДС самоиндукции

равна напряжению q/C на конденсаторе.

Имеем два уравнения:

Подставляя первое уравнение во второе, получаем уравнение для изменения заряда на конденсаторе:

Вместо использованной подстановки выражения тока через заряд можно продифференцировать второе из уравнений (1.15) и выразить производную от заряда через ток. В результате получим аналогичное уравнение для изменения тока в цепи:

с тем же выражением для , что и в (1.16).