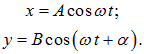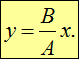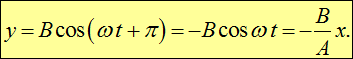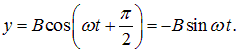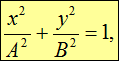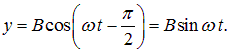1.5. Сложение взаимно перпендикулярных колебаний

В этом разделе мы рассмотрим сложение двух гармонических колебаний одинаковой частоты , происходящих во взаимно перпендикулярных направлениях вдоль осей x и y. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю:

где  — разность фаз обоих колебаний. Найдем уравнение траектории колеблющейся материальной точки, то есть функцию .

Рассмотрим сначала частные случаи. Пусть разность фаз равна нулю: . Тогда

то есть траектория точки представляет собой прямую. Аналогичная траектория получится при колебаниях с разностью фаз  

 При разности фаз  находим:

Из (1.58) и (1.55) следует уравнение эллипса:

причем точка движется по часовой стрелке (для стандартного направления осей: ось ОХ — направо, ось ОУ — вверх). При разности фаз  находим:

Это приводит к той же эллиптической траектории (1.59), только вращение в этом случае происходит против часовой стрелки.

Если амплитуды колебаний по осям х и у одинаковы (), то из (1.59) получается круговая траектория.

В общем случае произвольной разности фаз  траектория также будет представлять собой эллипс, но с повернутыми осями (рис. 1.18).

 

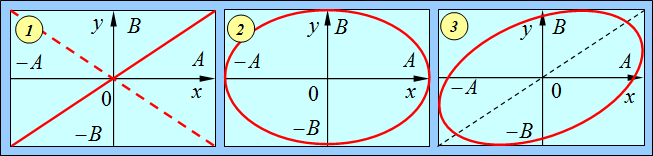
Рис. 1.18. Траектории материальной точки, колеблющейся с одинаковыми частотами
в перпендикулярных направлениях, при различных разностях фаз:
1 —    или   (штриховая линия); 3 —   ; 2 — 

Видео 1.15 Маятник Айри: запись песком фигур Лиссажу

Видео 1.16 Фигуры Лиссажу на экране осциллографа

Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет довольно сложный вид. Замкнутые траектории, описываемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, возникают тогда, когда отношение частот складываемых колебаний есть рациональное число, называются такие траектории  фигурами Лиссажу.

Одна из простейших фигур Лиссажу получается при отношении частот 2:1 и нулевых начальных фазах :

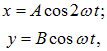
откуда

Мы получили уравнение параболы.

Форма фигур Лиссажу зависит от соотношения частот складываемых колебаний и разности фаз между ними. Примеры сложения колебаний с различными соотношениями частот показаны на рис. 1.19 и 1.20.

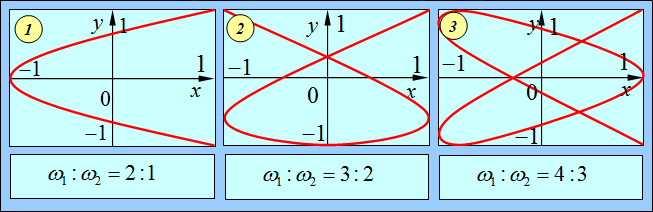
Рис. 1.19. Примеры фигур Лиссажу для указанных отношений частот и нулевых значений начальных фаз каждого колебания.
Координата x выражена в единицах амплитуды колебаний A, координата y – в единицах амплитуды B.
Частота   относится к колебаниям вдоль оси x,  – вдоль оси y

 

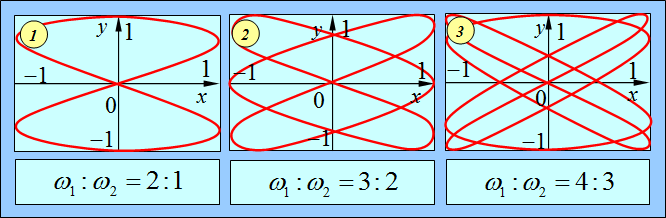
Рис. 1.20. Примеры фигур Лиссажу для тех же отношений частот, что на рис. 1.19 и одинаковых же начальных фазах каждого колебания , то есть при

 

Дополнительная информация

http://www.youtube.com/watch?v=DXpntnHxNZQ – Фигуры Лиссажу. Видео.

http://www.galileo-tv.ru/node/2426 – Видео из передачи «Галилео». Фигуры Лиссажу.

http://arbuz.uz/w_lisagu.html – Фигуры Лиссажу: первая любовь каждого программиста.

http://ligis.ru/effects/science/250/index.htm – Статья с анимацией о фигурах Лиссажу.