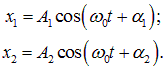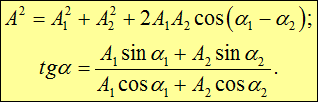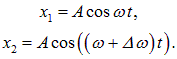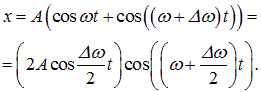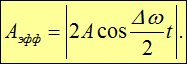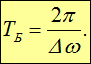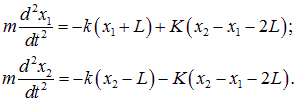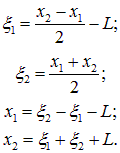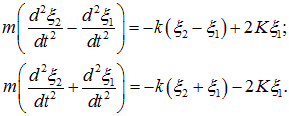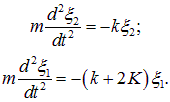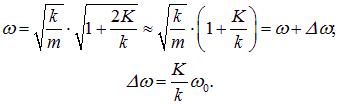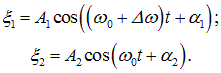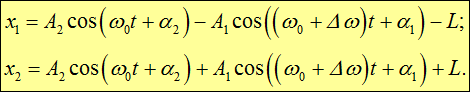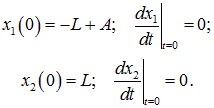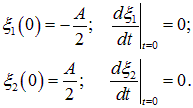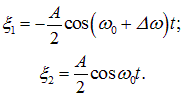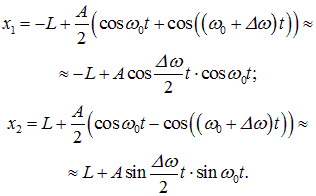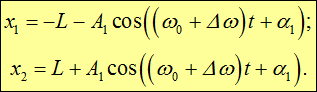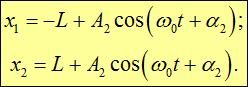1.4. Сложение колебаний одного направления

Может случиться так, что осциллятор принимает участие в двух одинаково направленных колебаниях с разными амплитудами, частотами и начальными фазами. Рассмотрим сложение таких колебаний.

Сложение колебаний с одинаковыми частотами

Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:

где x₁, x₂ — переменные, описывающие колебания, A₁, A₂ — их амплитуды, а  ,  — начальные фазы. Результирующее колебание

удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.

Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца этого вектора будет перемещаться по оси 0x от +A до –A, причем величина проекции будет изменяться по закону

Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).

 

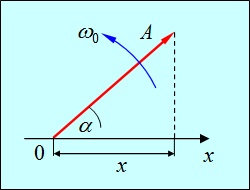
Рис. 1.12. Векторная диаграмма для общего решения (1.23)

Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А₁ и А₂  Возьмем их векторную сумму (рис. 1.13)

  

Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты

Проекция вектора А₁ на ось 0x равна сумме проекций соответствующих векторов

Таким образом, вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой A и начальной фазой a. Согласно теореме косинусов:

В частности, если фазы складываемых колебаний равны или отличаются на величину, кратную   (то есть ), то амплитуда результирующего колебания равна сумме амплитуд

Если же складываемые колебания находятся в противофазе (то есть ), то

Биения

В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте. Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые биениями.

Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно,  и . Итак,

Складываем эти выражения и учитываем известную формулу тригонометрии:

Если  то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:

Кроме того, множитель в скобках меняется медленно по сравнению с . Поэтому результирующее колебание x можно рассматривать как модулированное гармоническое колебание с частотой w, эффективная амплитуда  которого изменяется со временем по закону (1.40) (рис. 1.14):

Подчеркнем, что в строгом смысле такое колебание не является гармоническим, и еще раз напомним, что, согласно определению, колебание гармоническое, если оно происходит по закону , причем все три его параметра:  строго постоянны во времени.

Рис. 1.14. Биения при сложении колебаний с близкими частотами 

Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен

Видео 1.12 Биения на экране осциллографа

Видео 1.13 Биения: осциллограф и динамик

Видео 1.14 «Двойной» маятник: запись песком картины биений

Колебания двух связанных осцилляторов

Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться под действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<<k. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).

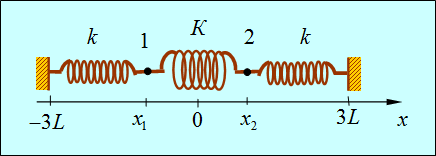
Рис. 1.15. Пример связанных осцилляторов.
Колебания происходят вдоль оси 0х, сила тяжести не учитывается 

Тогда в положении равновесия координаты грузов равны

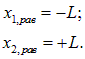
При колебаниях координаты равны, соответственно, x₁(t), x₂(t). Удлинения пружин записываются как

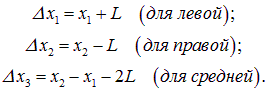
Мы имеем дело с системой с двумя степенями свободы. Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная

и сила со стороны пружины K, равная

На второй груз действуют аналогичные силы

и

Соответственно, уравнения движения имеют вид

Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x₁ оказывают влияния колебания x₂ и наоборот. Поэтому преобразуем уравнения к новым переменным, уравнения для которых были бы независимыми (такие переменные называют нормальными координатами, а соответствующие им колебания — нормальными  колебаниями (модами)). Именно, введем новые переменные x₁  и x₂:

Как легко убедиться, положениям равновесия соответствуют нулевые значения этих координат

В этих переменных уравнения (1.42) принимают вид:

Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для введенных нормальных координат:

Первое уравнение описывает гармонические колебания с частотой

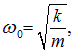
совпадающей с частотой колебаний пружинных маятников в отсутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой

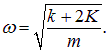
Так как K<<k, имеем

Соответственно, мы получаем общее решение системы уравнений:

Общее решение для координат х₁ и х₂ колеблющихся точек следуют из (1.47) и (1.43):

Для примера рассмотрим случай, когда первая масса смещается на расстояние  от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:

Этому соответствуют следующие начальные значения нормальных координат:

 Такие начальные условия уже рассматривались выше. Соответствующие им решения имеют вид

Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие колебания рассматриваемых масс около их положений равновесия:

 Графики функций x₁(t), x₂(t) показаны на рис. 1.16. Видна характерная картина биений.

 

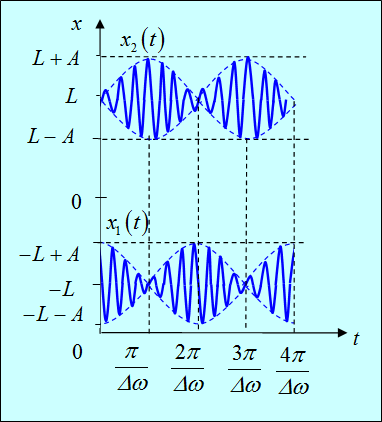
Рис. 1.16. Биения в системе двух связанных осцилляторов

В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время  первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту  первый маятник колеблется с максимальной амплитудой, а второй покоится.

На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.

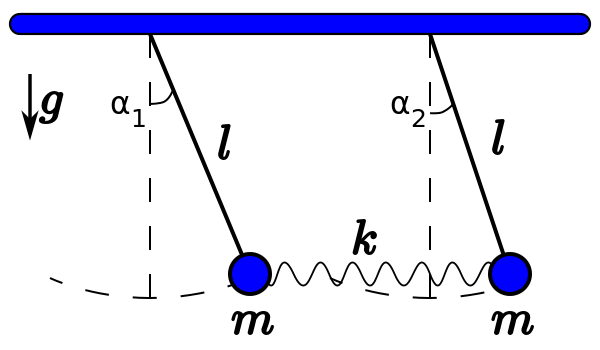
Рис. 1.17. Биения в системе связанных маятников

Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x₁), то A₂ = 0 и, как следует из общего решения (1.48),

Из (1.53) видно, что первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны, другими словами — они колеблются в противофазе. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов

Возбуждение только второй (x₂) нормальной моды означает, что A₁ = 0:

В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния, другими словами – они колеблются синфазно. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.

В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.

 

Дополнительная информация

http://allphysics.ru/feynman/bieniya — Фейнмановские лекции по физике. Биения.