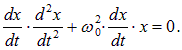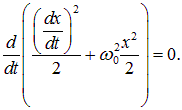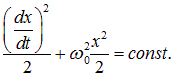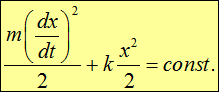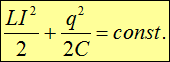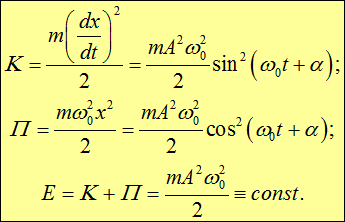1.3. Сохранение энергии при гармонических колебаниях
Умножим уравнение (1.18) гармонических колебаний на скорость изменения переменной x:
|
|
|
(1.28) |
Каждое из слагаемых можно представить как соответствующую производную:
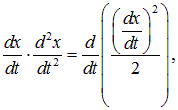
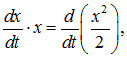
так что уравнение (1.28) записывается в виде:
|
|
|
(1.29) |
Отсюда следует, что величина в скобках не зависит от времени, то есть сохраняется в процессе колебаний:
|
|
|
(1.30) |
Для выяснения физического смысла сохраняющейся величины применим эти соотношения к пружинному маятнику, когда
![]()
Видим, что уравнение (1.30) можно записать в виде суммы кинетической энергии груза и потенциальной энергии деформированной (сжатой или растянутой) пружины:
|
|
|
(1.31) |
Таким образом, найденный закон сохранения есть не что иное, как закон сохранения полной энергии системы.
Аналогично, для электромагнитного контура переменная
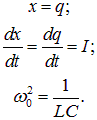
и
![]()
В этом случае соотношение (1.30) принимает вид:
|
|
|
(1.32) |
Первый член — это энергия магнитного поля в катушке, а второй — энергия электрического поля в конденсаторе. Снова мы получили, что сохраняется полная энергия системы.
Возвращаясь к общей форме (1.30) закона сохранения энергии и подставляя сюда общее решение (1.23), получаем законы изменения во времени кинетической и потенциальной энергий (или их аналогов) и выражение для сохраняющейся полной энергии:
|
|
|
(1.33) |
Отсюда следует, что
-
кинетическая и потенциальная энергии — периодические функции времени с периодом, равным половине периода колебаний;
-
кинетическая и потенциальная энергии колеблются в противофазе: когда кинетическая энергия достигает максимума, значение потенциальной энергии минимально и наоборот;
-
в колебательной системе энергия периодически «перекачивается» из одной формы в другую, а полная энергия Е = К + П сохраняется;
-
полная энергия колебаний пропорциональна квадрату их амплитуды и квадрату частоты.
Видео 1.9 Сохранение энергии при почти гармонических колебаниях – маятник Галилея.
Сказанное проиллюстрировано на рис. 1.11, на котором показаны изменения кинетической и потенциальной энергий для пружинного маятника и электромагнитного контура.

Рис. 1.11. Изменения во времени различных форм энергии в колебательной системе:
1 – пружинный маятник; 2 – электромагнитный колебательный контур
Видео 1.10 Cохранение энергии при механических колебаниях — маятник Максвелла
Видео 1.11 Cохранение энергии (и не только) при механических колебаниях — баллистический маятник