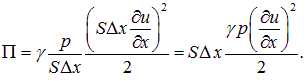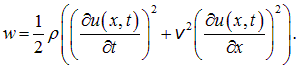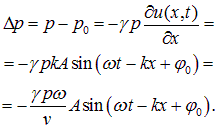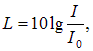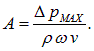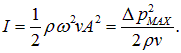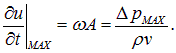2.3. Энергия волны

Рассмотрим для примера звуковую волну. Элемент объема на рис. 2.2. имеет кинетическую энергию:

При его деформации в данном объеме газа запасается потенциальная энергия П. Рассматривая колебания поршня, мы получили выражение (1.13) для силы упругости при перемещении поршня на расстояние х:

Этот закон аналогичен закону Гука для силы упругости при сжатии или растяжении пружины. Следовательно, потенциальная энергия газа равна в данном случае

Произведение  равно изменению объема газа под поршнем. Поэтому (3.35) можно записать в виде:

Применим это выражение к объему газа в звуковой волне. Давление в стационарном состоянии мы обозначили . Объем в стационарном состоянии равен . Изменение объема при колебаниях равно

Получаем тогда для потенциальной энергии данного объема газа:

Сумма кинетической и потенциальной энергии равна полной энергии данного объема. Плотность энергии w в волне получаем, разделив полную энергию на величину объема:

Учитывая, что фазовая скорость волны равна

записываем (2.38) в виде:

Точно такое же выражение получается для волны в твердом теле (неважно, продольной ли, поперечной ли) и для волны вдоль струны.

Подставляя сюда решение (2.22)

для монохроматической волны и учитывая соотношение

получаем для объемной плотности кинетической и потенциальной энергий одинаковые выражения

так что их сумма есть

Плотность энергии волны различна в разных точках пространства и в разные моменты времени. Зафиксируем какую-то точку х и усредним плотность энергии в данной точке по времени. Среднее значение квадрата синуса равно 1/2. Получаем тогда, что

Таким образом, среда обладает полным запасом энергии, плотность которой пропорциональна плотности среды, квадрату циклической частоты и квадрату амплитуды. Напомним, что для колебания системы с одной степенью свободы энергия колебания также была пропорциональна квадрату частоты и квадрату амплитуды колебания, а на месте плотности, — стояла масса колеблющегося тела.

Если вернуться к выражению (2.40) для мгновенного значения плотности энергии, то легко убедиться, что любое взятое значение плотности энергии, например, ее максимум

перемещается вдоль оси х с фазовой скоростью волны скоростью v. Иными словами, волна переносит энергию. Эта энергия доставляется, естественно, от источника колебаний. Можно ввести также вектор плотности потока энергии

модуль которого численно равен энергии, переносимой в единицу времени через единичную площадку, ортогональную направлению распространения волны. Отметим, что приведенные выше соотношения предполагают равенство скорости   переноса волной энергии фазовой скорости   волны. Это имеет место лишь в том случае, когда нет дисперсии, то есть фазовая скорость волны не зависит от её волнового числа, а именно, когда .

Применения к звуковой волне

Смещение частиц газа описывается стандартным решением:

где фазовая скорость

Под р и  понимаются давление и плотность невозмущенного волной газа.

Смещение частиц приводит к появлению избыточного давления

Здесь мы использовали соотношение (2.4).

Учитывая, что

формулу (2.42) можно переписать в виде:

Заметим, что колебания давления сдвинуты на  по отношению к колебаниям смещения частиц газа. При максимальном смещении

давление равно стационарному значению, то есть

Наоборот, амплитуда давления достигает максимума при нулевом смещении частиц газа.

Интенсивность волны, так же, как и объемная плотность энергии, пропорциональна квадрату амплитуды.

Звуковые волны принято характеризовать уровнем громкости L, измеряемым в децибелах (дБ). Связь уровня громкости с интенсивностью звуковой волны дается формулой:

где

Выбор I₀ связан с порогом слышимости в области частот 1 000 Гц – 4 000 Гц, к которым наиболее восприимчиво ухо человека. Таким образом, при I = I₀ уровень громкости полагается равным нулю. При интенсивностях волны порядка

волна перестает восприниматься как звук, вызывая только ощущение боли. Этому соответствует уровень громкости

Найдем связь между интенсивностью звуковой волны, избыточным давлением , создаваемым ею, и смещениями частиц газа. Амплитуда колебаний давления в волне равна (см. (2.43)):

откуда

Интенсивность волны выражаем также через амплитуду давления:

Отсюда находим избыточное давление в звуковой волне:

Учитывая, что плотность воздуха при нормальных условиях равна  кг/м³, получаем амплитуду колебаний давления на болевом пороге (L = 120 дБ, I = 1Вт/м²):

Амплитуда смещения частиц газа зависит при этом от частоты:

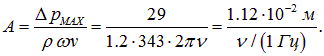
Отсюда следует, что при громкости L = 120 дБ и частоте n = 20 Гц смещение составляет А = 5.6·10^-4 м = 0.56 мм, а на частоте n = 20 кГц — А=5.6·10^-7 м = 0.56 мкм.

Найдем теперь амплитуду колебания скорости частиц газа:

Она не зависит от частоты волны и при громкости L = 120 дБ равна:

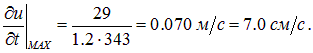
В таблице 1 представлены значения уровня громкости для некоторых звуков, с помощью которых можно найти избыточное давление, смещения и скорости частиц газа в иных случаях.

 

Таблица 1

Уровни громкости некоторых звуков 

 

Дополнительная информация

http://koi.tspu.ru/waves/ch4_4.htm – Кратко об энергии волны.

http://www.popmech.ru/article/9454-energiya-voln/ – Энергия волн: питание из воздуха. Статья из журнала «Популярная Механика»