2.4. Стоячие волны
Помимо бегущих волн предыдущего раздела, в природе существуют и стоячие волны, образующиеся в результате суперпозиции бегущих. Мы постоянно встречаемся с ними в своей практической жизни: когда говорим, поем, слушаем музыку. В этом разделе, после общих математических формул, мы совсем коротко обсуждаем некоторые вопросы музыкальной акустики – в надежде, что эта часть не покажется нашим студентам самой скучной.
Струна, закрепленная на одном конце
Предположим, что струна закреплена неподвижно в точке с координатой ![]() и тянется в положительном направлении оси х. Пусть по струне справа налево (то есть в отрицательном направлении оси х) распространяется волна
и тянется в положительном направлении оси х. Пусть по струне справа налево (то есть в отрицательном направлении оси х) распространяется волна
|
|
|
(2.50) |
Дойдя до точки закрепления, волна отразится. Если пренебречь потерями энергии, то амплитуда отраженной волны совпадет с амплитудой падающей волны. Надо учесть также, что при отражении происходит изменение направления движения элемента на обратное (как в упругом ударе шарика о стенку):
|
|
|
(2.51) |
Суперпозиция падающей и отраженной волн имеет вид:
|
|
|
(2.52) |
Мы видим, что в любой момент времени
![]()
Это и есть условие закрепления струны в точке ![]() . Воспользовавшись известными формулами тригонометрии для преобразования разности косинусов, записываем (2.53) в виде:
. Воспользовавшись известными формулами тригонометрии для преобразования разности косинусов, записываем (2.53) в виде:
|
|
|
(2.53) |
где ![]() — наибольшее смещение в стоячей волне.
— наибольшее смещение в стоячей волне.
Мы нашли особый тип колебаний: в каждой точке пространства струна колеблется с частотой ![]() и амплитудой
и амплитудой ![]() , причем все точки струны одновременно достигают своих максимальных отклонений (или проходят положение равновесия), и если мы находимся, например, в узле струны, то есть в точке с координатой
, причем все точки струны одновременно достигают своих максимальных отклонений (или проходят положение равновесия), и если мы находимся, например, в узле струны, то есть в точке с координатой
![]()
то в любой момент времени эта точка остается узлом. Иными словами, здесь нет движения волны, точки узлов волны (нулевых значений смещения) неподвижны, равно как и точки ее максимумов. Такие колебания и называются стоячими волнами.
|
Стоячая волна — периодическое колебание с характерным пространственным распределением амплитуды – чередованием узлов (нулей) и пучностей (максимумов). В одномерных (линейных) системах может быть представлена как сумма двух бегущих волн, распространяющихся навстречу друг другу. |
|
В стоячей волне плотность энергии меняется от точки к точке и зависит от времени, но в отличие от бегущей волны, здесь нет переноса энергии. |
Это очевидно хотя бы потому, что точки узлов волны неподвижны, и переноса энергии через них быть не может. Можно рассуждать и иначе: две бегущие волны, образовавшие стоячую, переносят одну и ту же энергию, но в противоположных направлениях, так что оба эти процесса взаимно компенсируются.
На рис. 2.9 показано образование стоячей волны при сложении двух бегущих навстречу друг другу монохроматических волн.

Рис. 2.9. Возникновение стоячей волны
Видео 2.3 Поперечные стоячие волны на линейке со свободным концом.
Видео 2.4 Поперечные стоячие волны на резиновом шнуре с закрепленными концами.
Видео 2.5 Поперечные стоячие волны на проводе с переменным током.
Подставляя найденное решение (2.53) в выражение (2.39), получаем для мгновенного значения плотности энергии стоячей волны выражение
|
|
|
(2.54) |
Усредняя по времени, находим:
|
|
|
(2.55) |
Мы получили, что средняя плотность энергии стоячей волны не зависит от точки наблюдения и равна сумме средних плотностей энергий двух бегущих волн, суперпозицией которых она является.
Пример 1. Для струны, закрепленной на одном конце, найдем точки, в которых плотность энергии колебаний не зависит от времени.
Используя соотношение
![]()
представим (2.54) в виде:
|
|
|
(2.56) |
Теперь ясно, что зависимости от времени не будет, если
![]()
или
![]()
то есть в точках
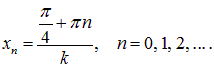
Пример 2. Найдем закон изменения во времени плотности энергии стоячей волны в точках, где смещение струны достигает своих максимальных значений.
Указанные точки имеют координаты
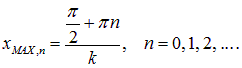
В этих точках
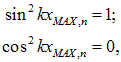
так что из (2.54) следует:
|
|
|
(2.57) |
Дополнительная информация
http://www.youtube.com/watch?v=DTKsn0ZaDoU – Образование стоячих волн. Видео.



