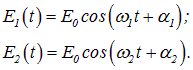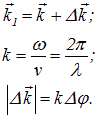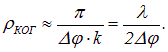4.2. Когерентность световых волн

Монохроматическая плоская электромагнитная волна описывается следующим выражением для напряженности поля в любой точке пространства, определяемой радиус-вектором r:

где Е₀, ,  и  являются постоянными величинами. Однако всякая реальная световая волна образуется наложением колебаний различных частот, заключенных в конечном интервале . Согласно формуле разбросу частот  соответствует разброс значений волнового числа . Следует отметить, что разброс волнового вектора может быть связан также с разбросом направлений распространения волн, который характеризуется векторной величиной .

Сначала обсудим временную когерентность, которая связана с разбросом частот . Рассмотрим случай наложения в некоторой точке пространства двух световых колебаний с несколько различающимися частотами :

Интерференционный член

при сделанных предположениях будет зависеть от времени и разности частот

Всякий оптический прибор, с помощью которого наблюдается интерференция света (фотопленка, человеческий глаз и др.), обладает определенной инертностью, которая характеризуется временем  регистрации прибором интерференционной картины. При этом оптический прибор регистрирует картину, усредненную по промежутку времени . Если за это время косинус в интерференционном члене

с равной вероятностью принимает все значения от –1 до +1, то среднее значение интерференционного члена будет равно нулю. Интерференционная картина не будет видна, то есть регистрируемая прибором интенсивность окажется равной сумме интенсивностей, создаваемых в данной точке каждой волной в отдельности. Если же за время  значение косинуса остается практически неизменным, то прибор зарегистрирует интерференцию. Таким образом, для характеристики когерентных свойств световых волн вводится время когерентности , которое определяется как время, за которое изменение разности фаз волн, накладывающихся в данной точке пространства, достигает значения :

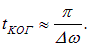
При

прибор не зафиксирует интерференцию, а при

прибор обнаружит интерференционную картину. За время когерентности  волна распространяется на расстояние

называемое длиной когерентности.

Для наблюдения интерференционной картины обычно используют пучки света от одного источника, но прошедшие разные расстояния до точки наблюдения. Это означает, что интерферируют волны, испущенные источником в разное время. Если частота источника «плавает», то при разности хода волн до точки наблюдения  разница во времени испускания волн будет , что означает невозможность наблюдения интерференции.

В качестве примера укажем типичные значения длины когерентности для естественного оптического источника с узкополосным светофильтром с шириной полосы пропускания  вблизи середины видимого диапазона ( нм) и для газового лазера — источника оптического излучения с высокой временной когерентностью, для которого ширина полосы на два-три порядка меньше. В первом случае оценка длины когерентности даёт значение

а во втором случае — для лазера —

Видео 4.3 Интерферометр Маха-Цандера.

Таким образом, наблюдение интерференционной картины от обычных оптических источников возможно лишь при малых разностях хода волн, например, при интерференции в тонких пленках, в то время как использование лазерного излучения существенно упрощает эту задачу.

В идеализированном случае при наложении монохроматических воли со строго фиксированными и равными частотами () время и длина когерентности становятся бесконечно большими, поэтому, естественно, в таких условиях интерференционная картина наблюдалась бы при любых разностях хода.

Изменение разности фаз колебаний может происходить не только из-за разбросa частот , но и вследствие разброса волновых векторов . Поэтому наряду с временной когерентностью, определяемой временем когерентности, вводится понятие пространственной когерентности. Возникновение в некоторой точке пространства колебаний, возбуждаемых волнами с целым набором различных по направлению векторов , имеет место, если эти волны испускаются различными участками протяженного источника света.

Рассмотрим для определенности светящийся диск АВ, который из точки М виден под углом  (рис. 4.1)

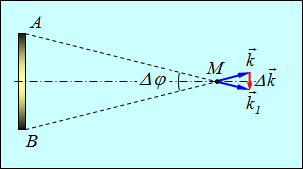
Рис. 4.1. Пространственная когерентность света от протяженного источника:
угол   характеризует разброс волновых векторов Ак 

Угол   характеризует разброс волновых векторов . Таким образом, в фазу электромагнитной волны

надо подставить выражения:

Тогда

так что

где   — проекция радиус-вектора r на направление вектора . В формулах (4.7) и ниже предполагается, что . Вектор , как видно из рисунка, можно считать параллельным протяженному источнику, и, соответственно, фронту волны.

Следовательно, фаза колебаний при переходе от одной точки волновой поверхности к другой изменяется. Введем расстояние , при смещении на которое вдоль волновой поверхности изменение фазы достигает значения :

откуда

Расстояние  характеризует пространственную когерентность волны и называется радиусом когерентности.

Видео 4.4 Интерференция двух волн. Бипризма Френеля.

Пусть длина  характеризует пространственное разрешение фотопленки или человеческого глаза. Интерференционный член усредняется по части пространства с линейными размерами порядка . При

среднее значение косинуса равно нулю, что не позволяет наблюдать интерференцию. В противоположном случае, когда

наблюдается чёткая интерференционная картина.

Приведем пример. Угловой размер Солнца

,

примерно в середине видимого диапазона длина волны видимого света

Следовательно, радиус когерентности приходящих от Солнца световых волн примерно равен

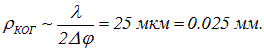
При таком малом радиусе когерентности невозможно непосредственно наблюдать интерференцию солнечных лучей, поскольку разрешающая способность человеческого глаза составляет лишь 0.1 мм. Однако в 1807 г. Т. Юнг провел первое наблюдение интерференции именно с солнечным светом. Для этого он пропускал солнечные лучи в темную комнату через маленькое отверстие, сделанное тонкой иглой. Отверстие на несколько порядков уменьшало угловой размер  источника света и, соответственно, увеличивало радиус когерентности.

 

Дополнительная информация

http://www.youtube.com/watch?v=B_adbUr8RHw – Пространственная когерентность. Презентация.